Ātrās kārtošanas algoritms

Ātrās kārtošanas algoritms ir kārtošanas algoritms, kuru izstrādāja Sers Čārlzs Antonijs Ričards Hoars (C.A.R. Hoare) Britu datorzinātnieks 1960. gadā kad bija 26 gadus vecs, un tas ir viens no plašāk izmantotajiem kārtošanas algoritmiem. Šī algoritma vidējā sarežģītība ir . Sliktākajā gadījumā algoritma sarežģītība ir tomēr, ja algoritmu lieto pareizi, tad šāds gadījums ir novērojams reti. Parasti ātrās kārtošanas algoritms ir ātrāks kā citi sarežģītības kārtošanas algoritmi, galvenokārt tādēļ, ka algoritma iekšējais cikls ir viegli uzlabojams un piemērojams nepieciešamajam gadījumam. Ātrās kārtošanas algoritma labās īpašības ir kārtošana bez papildu atmiņas (tiek izmantots neliels steks), mazais salīdzināšanu skaits, kā arī algoritma īsais iekšējais cikls.
Vēsture[labot šo sadaļu | labot pirmkodu]
Ātrās kārtošanas algoritmu izstrādāja Sers Čārlzs Antonijs Ričards Hoars (C.A.R. Hoare) Britu datorzinātnieks 1960. gadā kad bija 26 gadus vecs, un tas ir viens no plašāk izmantotajiem kārtošanas algoritmiem. Tas tika izstrādāts, laikā kad tā autors atradās Padomju Savienībā Maskavas Universitātē kā apmaiņas students, algoritma mērķis bija sakārtot tulkot nepieciešamos vārdus tā, lai tie būtu vienkāršāk saistīti savā starpā.
Algoritms[labot šo sadaļu | labot pirmkodu]

Algoritmam pamatā ir trīs soļi:
- Izvēlēties dalītāju (pivot) no faila.
- Pārkārtot failu tā, lai labajā pusē dalītājam (pivot) atrastos visi faila elementi, kas ir par to lielāki un kreisajā pusē visi elementi, kas ir mazāki.
- Rekursīvi izsaukt algoritmu katrai no izveidotajām faila daļām.
Algoritms ir balstīts uz ideju, ka apmaiņas darbības ieteicams veikt lielos attālumos, lai tās būtu visefektīvākās. Algoritma ātrdarbība lielā mērā atkarīga no tā, kādās daļās tiek sadalīts kārtojamais fails izpildot dalīšanas funkciju, kas savukārt atkarīgs no izvēlētā dalītāja (pivot). Ideāli būtu, ja katrā dalīšanas reizē fails tiktu sadalīts tieši uz pusēm, taču ne vienmēr ir pieejama nepieciešamā informācija, kuru elementu izvēlēties par dalīšanas elementu, lai panāktu ideālo sadalījumu. Nejaušam failam ir pilnīgi vienalga, kuru elementu izvēlas par dalīšanas elementu, jo ar jebkuru elementu kā dalīšanas elementu nejaušs fails tiks sadalīts vienādās daļās vidējā gadījumā.
Vienkāršā versija[labot šo sadaļu | labot pirmkodu]
Vienkāršā pseidokodā algoritms var tikt izteikts sekojoši:
function quicksort(masivs)
var list mazaks, lielāks
if length(masivs) ≤ 1
return masivs
select and remove a pivot value pivot from masivs
for each x in masivs
if x ≤ pivot then append x to mazaks
else append x to lielāks
return concatenate(quicksort(mazaks), pivot, quicksort(lielaks))
Jāievēro, ka vienkāršajā algoritma variantā elementi tiek pārbaudīti, tikai salīdzinot tos ar citiem elementiem, kas padara ātrās kārtošanas algoritmu par kārtošanu ar salīdzināšanu.
Algoritma pareizums ir balstīts uz sekojošiem argumentiem:
- Katrā iterācijā visi apstrādātie elementi nonāk to vēlamajā pozīcijā: mazākie pirms dalītāja (pivot), lielākie aiz dalītāja.
- Katra iterācija vismaz vienu elementu noliek tā galējā sakārtotajā pozīcijā.
Sarežģītā versija[labot šo sadaļu | labot pirmkodu]
Vienkāršās versijas mīnuss ir tāds, ka to izmantojot nepieciešama O(n) papildus atmiņa, kas ir tikpat daudz cik tiek izmantots kārtošanai ar sapludināšanu (merge sort). Papildus atmiņas prasība var būtiski ietekmēt algoritma darbības ātrumu un kešatmiņas darbību praktiskā algoritma pielietojumā. Lai novērstu vienkāršās versijas trūkumus ir izstrādāts ātrās kārtošanas algoritms, kurš spēj sakārtot datus vidēji izmantojot O(log n) papildus atmiņu. Ātrās kārtošanas algoritma dalīšanas funkcijas pseidokods izskatās sekojoši:
function partition(array, left, right, pivotIndex)
pivotValue := array[pivotIndex]
swap array[pivotIndex] and array[right] // Pārvietot dalītāju uz beigām
storeIndex := left
for i from left to right - 1 // left ≤ i < right
if array[i] ≤ pivotValue
swap array[i] and array[storeIndex]
storeIndex := storeIndex + 1
swap array[storeIndex] and array[right] // Pārvietot dalītāju uz tā gala pozīciju
return storeIndex
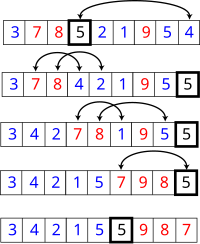
Šis dalīšanas algoritma pseidokods nav tāds kādu to izstrādāja Čārlzs Antonijs Ričards Hoars, pastāv vēl citas dalīšanas funkcijas priekš ātrās kārtošanas algoritma, tomēr šo saprast ir nedaudz vieglāk kā citas.
Kad dalīšanas funkcija ir izveidota uzrakstīt ātrās kārtošanas algoritmu vairs nav tik sarežģīti un tas ir sekojošs:
procedure quicksort(array, left, right)
if right > left
select a pivot index //(e.g. pivotIndex := left+(right-left)/2)
pivotNewIndex := partition(array, left, right, pivotIndex)
quicksort(array, left, pivotNewIndex - 1)
quicksort(array, pivotNewIndex + 1, right)
Tomēr tā, kā dalīšanas funkcija pārkārto elementus katrā daļā, tad šī ātrās kārtošanas algortima versija nav stabila.
Šī ir vēl viena ātrās kārtošanas algoritma versija, kas darbojas ar nelielu papildus atmiņu:
function quicksort(array, left, right)
var pivot, leftIdx = left, rightIdx = right
if right - left > 0
pivot = (left + right) / 2
while leftIdx <= pivot and rightIdx >= pivot
while array[leftIdx] < array[pivot] and leftIdx <= pivot
leftIdx = leftIdx + 1
while array[rightIdx] > array[pivot] and rightIdx >= pivot
rightIdx = rightIdx - 1;
swap array[leftIdx] with array[rightIdx]
leftIdx = leftIdx + 1
rightIdx = rightIdx - 1
if leftIdx - 1 == pivot
pivot = rightIdx = rightIdx + 1
else if rightIdx + 1 == pivot
pivot = leftIdx = leftIdx - 1
quicksort(array, left, pivot - 1)
quicksort(array, pivot + 1, right)
Dalītāja izvēle[labot šo sadaļu | labot pirmkodu]
Sākotnējā algoritma versijā par dalītāju tika izvēlēts kreisais pirmais elements no kārtojamo elementu saraksta, tomēr tāda dalītāja izvēle rada sliktākā varianta sarežģītību gandrīz sakārtotiem failiem, kas ir diezgan bieža parādība praktiskā pielietojumā. Šī problēma tika novērsta par izveidojot dalīšanas funkciju, kas par dalītāju katru reizi izvēlas nejaušu elementu, vidējo elementu, vai pēdējo elementu no faila.
Analīze[labot šo sadaļu | labot pirmkodu]
Sākotnējā variantā nav pārāk grūti saprast, ka ātrā kārtošana izmanto vidēji laiku. Tas ir saprotams, jo ir redzams, ka dalīšanas funkcija, kura iet cauri failam tikai vienreiz, izmanto laiku.
Labākajā sagaidāmajā variantā, katru reizi veidojot kārtojamā faila daļu, iepriekšējais fails tiek sadalīts divās aptuveni vienādās daļās, tas nozīmē, ka katrs rekursīvs izsaukums darbojas tikai ar pusi no iepriekšējā faila, līdz ar to var veikt tikai izsaukumus pirms tiek sasniegts fails ar garumu 1. Tas nozīmē, ka katra algoritma izsaukuma dziļums ir vienāds ar . Nepastāv divi vienādi izsaukumi, kuri apstrādātu vienādu faila daļu, tādējādi katram izsaukuma līmenim nepieciešams tikai laiks, rezultātā kopējais algoritms izmanto tikai laiku.
Alternatīvs novērtējuma variants ir izmantot rekurences () aprēķinu - laiku, kas nepieciešams, lai sakārtotu elementu garu failu. Rekurences aprēķina formula ir sekojoša:
Pamatteorēmā savukārt minēts, ka rekurence ir .
Sliktākajā gadījumā savukārt abu izveidoto faila daļu garumi ir 1 un (piemēram, dalītājs ir vislielākais skaitlis kārtojamajā failā) līdz ar to izsaukumu skaits pieaug līdz izsaukumiem. Tādā gadījumā rekurence ir sekojoša:
un rezultāts ir sekojošs:
Nepieciešams atcerēties, ka pastāv vairāki ātrās kārtošanas algoritma varianti, tajā skaitā arī nerekursīvs ātrās kārtošanas algoritms, izvēle paliek lietotāja ziņā, tomēr labu rezultātu var iegūt, ja par dalītāju katru reizi izsaucot algoritmu tiek izvēlēts nejaušs elements no kārtojamo elementu faila. Tādējādi algoritmā nepieciešams mainīt dalīšanas funkciju, tomēr izmantojot uzlabotu ātrās kārtošanas algoritmu līdz minimumam tiek samazināta iespēja rezultātā iegūt sliktākā gadījuma algoritma sarežģītību .
Varianti[labot šo sadaļu | labot pirmkodu]
Pastāv 3 labi zināmi ātrās kārtošanas algoritma varianti:
- Balansētā ātrā kārtošana dalītājs (pivot) katru reizi tiek piemeklēts tāds, lai tas būtu aptuveni tik liels kā vidējais elements no faila.
- Ārējā ātrā kārtošana tāds pats algortims kā parastais ātrās kārtošanas algoritms, tikai dalītājs tiek aizvietots ar buferi, fails tiek kārtots bufera atmiņā.
- Trīs-virzienu radix ātrā kārtošana (saukta arī multikey ātrā kārtošana) ir radix kārtošanas un ātrās kārtošanas apvienojums. Tiek izvēlēts elements no faila (dalītājs) un pirmais elementa simbols tiek izmantots kā atslēga. Atlikusī faila daļa tiek sadalīta 3 daļās: tādās, kuru atslēgas ir mazākas, vienādas vai lielākas ar dalītāja atslēgu. Rekursīvi tiek izsaukts algoritms daļām, kuru elementu atslēgas ir mazākas vai lielākas, pēc tam rekursīvi tiek izsaukts algoritms daļai, kurā elementu atslēgas bija vienādas, salīdzinot kārtojamo elementu otros simbolus.













