Pirmreizinātājs

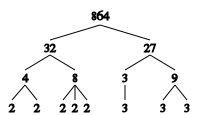
Pirmreizinātājs ir kāda naturāla skaitļa dalītājs, kas ir pirmskaitlis. Piemēram, skaitļa 12 pirmreizinātāji ir 2 un 3, bet skaitļa 25 vienīgais pirmreizinātājs ir 5. Skaitli sadalīt pirmreizinātājos nozīmē izteikt to kā vairāku pirmskaitļu reizinājumu, katram pirmskaitlim norādot arī kāpinātāju, ar kādu tas ietilpst dotajā skaitlī. Piemēram, 12 = 2² · 3, 7 = 7¹, 360 = 2³ · 3² · 5, utt. Aritmētikas pamatteorēma apgalvo, ka katru naturālu skaitli, kas lielāks par 1, var sadalīt pirmreizinātājos, turklāt vienā vienīgā veidā (neņemot vērā pirmreizinātāju kārtību). Skaitlim 1 nav pirmreizinātāju, jo tas dalās tikai ar 1, kas nav pirmskaitlis.

Izmantojot to, ka mazākais pirmskaitlis ir 2, var viegli pierādīt, ka jebkura naturāla skaitļa $n$ pirmreizinātāju skaits nepārsniedz [log₂ n].

Informācijas šifrēšana[labot šo sadaļu | labot pirmkodu]

Skaitļa $n$ sadalīšana pirmreizinātājos ir grūts uzdevums, sevišķi ja $n$ ir liels. Labākais patlaban zināmais algoritms šo uzdevumu veic subeksponenciālā laikā.^[1] Izmantojot pieņēmumu, ka skaitļa sadalīšanai pirmreizinātājos ir nepieciešams ļoti ilgs laiks, ir radītas grūti uzlaužamas šifrēšanas metodes. Kamēr netiks izveidots ātrs algoritms skaitļu sadalīšanai pirmreizinātājos, tikmēr šīs metodes ir praktiski neuzlaužamas. Populārākā no šīm metodēm ir RSA šifrēšanas algoritms.

Neskatoties uz to, ka joprojām nav zināms, kāds ir ātrākais algoritms skaitļu sadalīšanai pirmreizinātājos (lietojot tradicionālos datorus), ir pierādīts, ka ar kvantu datoru to ir iespējams izdarīt pietiekoši ātri (polinomiālā laikā). Pagaidām vēl nav uzbūvētas ierīces, kas to spētu izdarīt pietiekoši lieliem skaitļiem (pašreizējie kvantu datori spēj sadalīt pirmreizinātājos skaitli 15).^[2]

Skatīt arī[labot šo sadaļu | labot pirmkodu]

Atsauces[labot šo sadaļu | labot pirmkodu]

↑ Crandall, Richard E.; Pomerance, Carl (2005), Prime numbers: a computational perspective, Springer, ISBN 978-0-38-725282-7, Chapter 6, Subexponential factoring algorithms, 261. lpp.
↑ NMR quantum computing: Realizing Shor's algorithm, Nature, December 2001.

[1] Crandall, Richard E.; Pomerance, Carl (2005), Prime numbers: a computational perspective, Springer, ISBN 978-0-38-725282-7, Chapter 6, Subexponential factoring algorithms, 261. lpp.

[2] NMR quantum computing: Realizing Shor's algorithm, Nature, December 2001.

[1]

[2]