Apgrieztā proporcionalitāte

Apgrieztā proporcionalitāte ir funkcijas proporcionalitātes veids, ko var izteikt ar formulu $y={k \over x}$, kur $x$ ir neatkarīgais mainīgais, $y$ — atkarīgais mainīgais un $k$ — no nulles atšķirīgs reāls skaitlis. Sakarību starp apgriezti proporcionāliem lielumiem var izteikt pēc šādas pazīmes: Cik reižu viens lielums palielinās, tik reižu otrs lielums samazinās, un otrādi.

Funkcijas grafiks

Augoša funkcija

Dilstoša funkcija

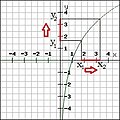
Funkcijas grafiks ir līkne, ko sauc par hiperbolu. Atkarībā no tā vai $k$ ir pozitīvs vai negatīvs, funkcija var būt vai nu augoša vai dilstoša.

Augoša funkcija

Augoša funkcija ir tad, ja $k<0$. Šīs funkcijas grafiks atrodas $II$ un $IV$ kvadrantā. Šādu funkciju sauc arī par daļveida negatīvu funkciju.

Dilstoša funkcija

Dilstoša funkcija ir tad, ja $k>0$. Šīs funkcijas grafiks atrodas $I$ un $III$ kvadrantā. Šādu funkciju sauc arī par daļveida pozitīvu funkciju.

Kvadrantu izvietojums koordinātu plaknē

Funkcijas īpašības

Definīcijas un vērtību apgabali

• Definīcijas apgabals ir visi reālie skaitļi, izņemot $0$ :

$D(f)$ $=(-\infty ;0)\cup (0;+\infty )$

• Vērtību apgabalsir visi reālie skaitļi, izņemot $0$ :

$D(f)$ $=(-\infty ;0)\cup (0;+\infty )$

Zaru vērsums

• Ja $a>0$, tad hiperbolas zari atrodas $I$ un $III$ kvadrantā, funkcija ir dilstoša
• Ja $a<0$, tad hiperbolas zari atrodas $II$ un $IV$ kvadrantā, funkcija ir augoša

Monotona funkcija

Ja funkcija kādā intervālā tikai aug vai dilst, tad to sauc par monotonu funkciju.

• funkciju sauc par augošu, ja, palielinoties argumenta vērtībām, palielinās funkcijas vērtības
• funkciju sauc par dilstošu, ja, palielinoties argumenta vērtībām, samazinās funkcijas vērtības

• 
  Monotona augoša funkcija
• 
  Monotona dilstoša funkcija

Funkcijas paritāte

• Apgrieztā proporcionalitāte ir nepāra funkcija.
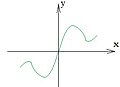
• Nepāra funkcijas grafiks ir centrāli simetrisks pret koordinātu sākumpunktu $(0;0)$
• Funkciju $y=f(x)$ sauc par nepāra funkciju, ja visiem $x$ no definīcijas apgabala
       $f(x)=f(-x)$
• Ja funkcija $f(x)$ uzdota analītiski (ar formulu), tad, lai pārbaudītu funkcijas paritāti, jārēķina funkcijas vērtība
        $f(-x)$

• 
  Nepāra funkcijas grafiks ir centrāli simetrisks pret koordinātu sākumpunktu $(0;0)$
• 
  Nepāra funkcija

Funkcijas grafika konstruēšana

Lai sāktu konstruēt hiperbolu, vērtību tabulā ir jāatliek vismaz 3 pozitīvas un 3 negatīvas vērtības. Lai sanāktu precīzāks grafiks, var atlikt vairāk vērtību.

Augošas funkcijas grafika konstruēšana

Augošas funkcijas grafiks

Lai konstruētu grafiku, piemēram, funkcijai $y={-1 \over x}$:

• Sastāda vērtību tabulu

X	-4	-2	-1	1	2	4
Y	0,25	0,5	1	-1	-0,5	-0,25

• Atliek atrastos punktus koordinātu plaknē
• Uzzīmē hiperbolu

Dilstošas funkcijas grafika konstruēšana

Dilstošas funkcijas grafiks

Lai konstruētu grafiku, piemēram, funkcijai $y={4 \over x}$:

• Sastāda vērtību tabulu

X	-4	-2	-1	1	2	4
Y	-1	-2	-4	4	2	1

• Atliek atrastos punktus koordinātu plaknē
• Uzzīmē hiperbolu

Ārējās saite

• Matemātikas teorija 10.klasei
• Vizuālie materiāli matemātikā 10.klasei
• Inverse Proportion

Skatīt arī

• Funkcija
• Hiperbola