Sinuss
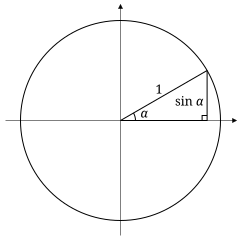
Par leņķa sinusu sauc uz tā balstīta taisnleņķa trijstūra pretkatetes un hipotenūzas garumu attiecību. To var simboliski pierakstīt šādi:
kur "sin α" apzīmē sinusu no leņķa α un "pretkatete" un "hipotenūza" apzīmē attiecīgi pretkatetes (leņķim pretējas katetes) un hipotenūzas garumus. Šādā veidā sinusu var definēt šauriem leņķiem. Savukārt, izmantojot trigonometrisko riņķi, sinusu var definēt jebkuram leņķim.
Sinusa funkcija ir periodiska funkcija ar periodu 2π.
Funkcijas nosaukuma pirmsākumi meklējami indiešu matemātiķa un astronoma Ārjabhatas darbos, kur tā saukta ardha-jya (tulkojumā - 'puse no hordas'), kas ērtības labad saīsināta par jya. Tulkojot Ārjabhatas darbus arābu valodā, saīsinājums tika pārnests ar līdzkaņu burtiem jb (arābu rakstībā īsos patskaņu neraksta, "b" rakstībā līdzīgs "y") un izrunāja ar vārdu jiba, kam valodā nav nozīmes. 12. gadsimtā, kad Gerardo no Kremonas tulkoja šos darbus latīņu valodā, viņš pieņēma, ka jb lasāms kā jiab ('līcis', 'ieloks') un pārcēla ar tā latīnisko analogu ar tādu pat nozīmi sinus.[1]
Sinusa vērtības[labot šo sadaļu | labot pirmkodu]
| Leņķis grādos | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| Leņķis radiānos | 0 | π/6 | π/4 | π/3 | π/2 |
| Sinusa vērtība |
Visbiežāk nepieciešamās sinusa vērtības ir dotas tabulā pa labi. Lai tās vieglāk iegaumētu, ir jāatceras zīmīgie leņķi 0°, 30°, 45°, 60° un 90° (jeb 0, π/6, π/4, π/3 un π/2 radiānos). Var ievērot, ka tiem atbilstošās sinusa vērtības ir šādas:
Leņķiem, kas neatrodas intervālā no 0° līdz 90°, sinusa vērtību var aprēķināt, izmantojot zemāk uzskaitītās sinusa funkcijas īpašības.
Sinusa funkcijas īpašības[labot šo sadaļu | labot pirmkodu]

Sinusa funkcijai piemīt vairākas būtiskas īpašības, kas ir uzskaitītas zemāk dotajā tabulā. Tās ir viegli nolasāmas no funkcijas grafika.
| Matemātiskais pieraksts | Īpašības nosaukums |
|---|---|
| ierobežota | |
| nepāra | |
| periodiska | |
| maina zīmi, ja leņķi palielina par π |
No šīm īpašībām izriet sakarība
kur k ir patvaļīgs vesels skaitlis. Ar tās palīdzību sinusa aprēķināšanu patvaļīgam leņķim var reducēt uz sinusa aprēķināšanu leņķim, kas atrodas intervālā [0°, 90°] (jeb [0,π/2] radiānos).
Sakarības[labot šo sadaļu | labot pirmkodu]
Jebkuriem diviem reāliem skaitļiem α un β ir spēkā:
Teilora rinda, atvasinājums un integrālis[labot šo sadaļu | labot pirmkodu]
Sinusa izvirzījums Teilora rindā ir
Tā atvasinājums ir
bet nenoteiktais integrālis ir
Skatīt arī[labot šo sadaļu | labot pirmkodu]
Atsauces[labot šo sadaļu | labot pirmkodu]
- ↑ Howard Eves. An Introduction to the History of Mathematics (6 izd.). Saunders College Publishing House, New York, 1990. 237. lpp.
Ārējās saites[labot šo sadaļu | labot pirmkodu]
- Eric W. Weisstein, Sine, MathWorld.


















