Tetramino
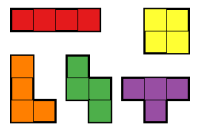
Tetramino ir polimino, kurš sastāv no četriem vienības kvadrātiem, kuri ir savienoti gar malām. Bez rotācijām un spoguļattēla simetrijām, pastāv pieci unikāli tetramino. Ar rotācijām un spoguļattēliem, kopā pastāv 19 tetramino pozīcijas.
Tetramino guva slavu no videospēles "Tetris", kurā tetramino sauc par tetrimino. Tetramino, kuri novērojami spēlē, ir bez spoguļsimetrijas.
Visi tetramino
[labot šo sadaļu | labot pirmkodu]Ir divi dažādi I-tetramino, četri J-tetramino, četri L-tetramino, viens O-tetramino, divi S-tetramino, četri T-tetramino un divi Z-tetramino, kopā 19 tetramino pozīcijas.
Taisnstūra pārklāšana ar tetramino
[labot šo sadaļu | labot pirmkodu]
Taisnstūra aizpildīšana ar vienu tetramino kopu
[labot šo sadaļu | labot pirmkodu]Viena kopa ar tetramino nevar ietilpt taisnstūrī. Šo var pierādīt aizkrāsojot figūras rūtiņas pēc šaha galda principa. 5x4 taisnstūrī šaha galdiņa nokrāsojumā būs 20 lauciņi, 10 gaiši un 10 tumši, bet pilna kopa ar tetramino aizklāj 11 tumšus un 9 gaišus lauciņus, jo T-tetramino aizkrāso 3 melnas un 1 gaišu rūtiņu.
Taisnstūra aizpildīšana ar vienu tetramino kopu taisntūros ar izmaiņām
[labot šo sadaļu | labot pirmkodu]
Visi tetramino spēj ietilpt taisnstūros ar caurumiem:
- Visi 5 unikālie tetramino ir piemēroti 7 × 3 taisnstūrim ar vienu caurumu.
- Visi 7 unikālie + spoguļattēla tetramino ir piemēroti 6 × 5 taisnstūrim ar diviem vienādas "šaha krāsas" caurumiem.
- Visi 19 tetramino pozīcijas ir piemērotas 11 × 7 taisnstūrim ar vienu caurumu.

7 tetramino aizpilda 5 x 6 taisnstūri ar diviem caurimiem.

