Dalībnieks:Elina.nesterenkova/Smilšu kaste
 | Šī ir dalībnieka Elina.nesterenkova smilšu kaste. Smilšu kaste ir dalībnieka lapu apakšlapa, kurā var tikt veikti dažādi eksperimenti. Šis nav enciklopēdijas raksts. Izveido pats savu smilšu kasti šeit. Raksta veidošanas procesā var noderēt lapas: "Raksta izveidošana", "Rakstu vednis", "Vikipēdijas palīdzība". |
Nevienādība ir apgalvojums, kurā tiek saildzināta divu lielumu savstarpējā vērtība.
Par lineāro nevienādību sauc nevienādību, kas uzrakstāma formā ax + b > 0, kur a un b doti skaitļi, bet x nezināmais.
Skaitļu intervāls
[labot šo sadaļu | labot pirmkodu]Par skaitļu intervālu sauc visus skaitļus, kam patiesa dota nevienādība un ko pieraksta sausinātā veida.
Patiesa un aplama nevienādība
[labot šo sadaļu | labot pirmkodu]- Nevienādība ir patiesa, jo 3 pieder intervālam.
- Nevienādība ir aplama , jo 3 nepieder intervālam.
Stingras nevienādības
[labot šo sadaļu | labot pirmkodu]Ja nevienādības pierakstā izmanto zīmes > vai < (lasa: lielāks vai mazāks), nevienādību sauc par stingru nevienādību.
- , nozīmē "a ir lielāks nekā b";
- , nozīmē "a ir mazāks nekā b".
Zīmējumā atliek skaitlisko vērtību, ievērojot, ka stingrām nevienādībām zīmē tukšu punktu ໐ un liek apaļas iekavas.
Nestingras nevienādības
[labot šo sadaļu | labot pirmkodu]Ja nevienādības pierakstā izmanto zīmes ≤ vai ≥ (mazāks vai vienāds; lielāks vai vienāds), nevienādību sauc par nestingru nevienādību.
- , nozīme "a ir vienāds vai lielāks nekā b";
- , nozīme "a ir vienāds vai mazāks nekā b".
Zīmējumā atliek skaitlisko vērtību, ievērojot, ka nestingrām nevienādībām zīmē pilnu punktu ● un liek kvadrātiekavas.
Skaitļu intervālu piemēri
[labot šo sadaļu | labot pirmkodu]Skaitlisku nevienādību īpašības
[labot šo sadaļu | labot pirmkodu]| Īpašība | Piemērs |
|---|---|
| 1)Ja patiesas nevienādības abām pusēm pieskaita
vai atņem vienu un to pašu skaitli, tad iegūst patiesu nevienādību. |
|
| 2) Ja patiesas nevienādības abas puses reizina
vai dala ar vienu un to pašu pozitīvu skaitli, tad iegūst patiesu nevienādību. |
|
| 3) Ja patiesas nevienādības abas puses reizina
vai dala ar vienu un to pašu negatīvu skaitli, nevienādības veidu maina uz pretējo. |
maina no uz
ja zīmi nemainīt, tad apgalvojums būtu aplams |
Nevienādību īpašības
[labot šo sadaļu | labot pirmkodu]Divas nevienādības ir ekvivalentas, ja tām ir vienādas atrisinājumu kopas.
Lineāru nevienādību atrisināšana
[labot šo sadaļu | labot pirmkodu]1.piemērs
[labot šo sadaļu | labot pirmkodu]Atrisināt nevienādību
Vienādojam saucējus, par kopsaucēju izvēloties 40.
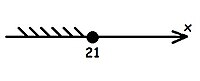
2.piemērs
[labot šo sadaļu | labot pirmkodu]Atrisināt nevienādību
















![{\displaystyle x\in (-\infty ;a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1340869d4ca63f0a4ead73ad883bd692ce33aa3b)





































![{\displaystyle x\in (-\infty ;21]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd7e115f557ede74f393ef613dd0d5b909f1486d)




