Lineāra nevienādība

Lineāra nevienādība ir nevienādība, kas uzrakstāma formā ax + b > 0, kur a un b ir doti skaitļi, bet x — nezināmais.

Skaitļu intervāls

Par skaitļu intervālu sauc visus skaitļus, kam patiesa dotā nevienādība un ko pieraksta saīsinātā veidā.

Patiesa un aplama nevienādība

${3\geqslant 3}$ - Nevienādība ir patiesa, jo 3 pieder intervālam.

${3>3}$ - Nevienādība ir aplama , jo 3 nepieder intervālam.

Stingras nevienādības

Ja nevienādības pierakstā izmanto zīmes > vai < (lasa: lielāks vai mazāks), nevienādību sauc par stingru nevienādību.

• ${a>b}$, nozīmē "a ir lielāks nekā b";
• ${a<b}$, nozīmē "a ir mazāks nekā b".

Zīmējumā atliek skaitlisko vērtību, ievērojot, ka stingrām nevienādībām zīmē tukšu punktu ໐ un liek apaļas iekavas.

Nestingras nevienādības

Ja nevienādības pierakstā izmanto zīmes ≤ vai ≥ (mazāks vai vienāds; lielāks vai vienāds), nevienādību sauc par nestingru nevienādību.

• ${a\geqslant b}$, nozīme "a ir vienāds vai lielāks nekā b";
• ${a\leqslant b}$, nozīme "a ir vienāds vai mazāks nekā b".

Zīmējumā atliek skaitlisko vērtību, ievērojot, ka nestingrām nevienādībām zīmē pilnu punktu ● un liek kvadrātiekavas.

Skaitļu intervālu piemēri

Nevienādības	a-skaitļa attēlojums uz skaitļu ass	Skaitļu intervāla pieraksts
${x>a}$	x ir lielāks nekā a	$x\in (a;+\infty )$
${y<a}$	y ir mazāks nekā a	$y\in (-\infty ;a)$
${x\geqslant a}$	x ir vienāds vai lielāks nekā a	$x\in (-\infty ;a]$
${y\leqslant a}$	x ir vienāds vai mazāks nekā y	$y\in [a;+\infty )$
${y\in \mathbb {R} }$	y ir jebkurš skaitlis	$y\in (-\infty ;+\infty )$

Skaitlisku nevienādību īpašības

Īpašība	Piemērs
1)Ja patiesas nevienādības abām pusēm pieskaita vai atņem vienu un to pašu skaitli, tad iegūst patiesu nevienādību.	$11>9$ $11+2>9+2$ $11+2-2>9+2-2$ $11>9$
2) Ja patiesas nevienādības abas puses reizina vai dala ar vienu un to pašu pozitīvu skaitli, tad iegūst patiesu nevienādību.	$2>6$ $2>6\mid \centerdot 3$ $6>18$ $6>18\mid :3$
3) Ja patiesas nevienādības abas puses reizina vai dala ar vienu un to pašu negatīvu skaitli, nevienādības veidu maina uz pretējo.	$-44\geqslant -33$ $-44\geqslant -33\mid :(-11)$ maina no $\geqslant$ uz $\leqslant$ $4\leqslant 3$ ja zīmi nemainīt, tad apgalvojums būtu aplams

Nevienādību īpašības

Divas nevienādības ir ekvivalentas, ja tām ir vienādas atrisinājumu kopas.

Īpašība	Piemērs	Zīmējums
1) Ja nosacītās nevienādības abām pusēm pieskaita vai atņem vienu un to pašu skaitli, tad iegūst dotajai nevienādībai ekvivalentu nevienādību	$x>9$ $x+2>9+2$ $x+2-2>9+2-2$ $x>9$	x ir lielāks nekā deviņi
2) Ja nosacītās nevienādības abas puses reizina vai dala ar vienu un to pašu pozitīvu skaitli, tad iegūst dotajai nevienādībai ekvivalentu nevienādību	$x>5$ $x>5\mid \centerdot 2$ $2x>10\mid :2$ $x>5$	x ir lielāks nekā pieci
3) Ja nosacītās nevienādības abas puses reizina vai dala ar vienu un to pašu negatīvu skaitli un nevienādības zīmi maina uz pretējo, tad iegūst dotajai nevienādībai ekvivalentu nevienādību.	$-2x\leqslant 8$ $-2x\leqslant 8\mid :(-2)$ maina zīmi no $\leqslant$ uz $\geqslant$ $x\geqslant 4$	x ir vienāds vai lielāks nekā 4

Lineāru nevienādību atrisināšana

1.piemērs

Atrisināt nevienādību ${\frac {x-1}{5}}-{\frac {x+3}{8}}\leqslant 1$

Vienādojam saucējus, par kopsaucēju izvēloties 40.

${\frac {8(x-1)}{40}}-{\frac {5(x+3)}{40}}\leqslant {\frac {40}{40}}\mid \centerdot 40$

$8(x-1)-5(x+3)\leqslant 40$

$3x-23\leqslant 40$

$3x-23+23\leqslant 40+23$

$3x\leqslant 63\mid :3$

$x\leqslant 21$

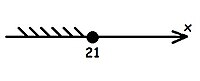x ir vienāds vai mazāks nekā 21

$x\in (-\infty ;21]$

2.piemērs

Atrisināt nevienādību $5x+7<13x-9$

$5x+7<13x-9$

$5x-13x<-9-7$

$-8x<-16\mid :(-8)$

$x>2$

$x\in (2;+\infty )$

Atsauces

• Inese Lude, Jolanta Lapiņa "Matemātika 7. klasei"; Pētergailis 2013. gads
• Inese Lude, Silva Januma "Algebra katrai stundai" ; Zvaigzne ABC 2002. gads
• Baiba Āboltiņa, Silva Januma "Matemātika 7.klasei" ; Zvaigzne ABC 2015. gads