Pentamino

Pentamino ir visi tie polimino, kas sastāv no tieši pieciem kvadrātiem. Turklāt pentamino netiek uzskatīti par dažādiem, ja tie iegūstami viens no otra ar pagriešanu vai "apgāšanu" (spoguļattēlošanu). Pastāv tikai divpadsmit unikāli pentamino. Lai saīsinātu pierakstus, pentamino apzīmēšanai bieži lieto burtus F, I, L, N, P, T, U, V, W, X, Y un Z. Saskaitot visas iespējamās pozīcijas, iegūst 63 pentamino pozīcijas.
Vēsture[labot šo sadaļu | labot pirmkodu]
Ar polimino, kas ir vispārīgāks jēdziens nekā pentamino, nesaraujami ir saistīts amerikāņu zinātnieka Solomona Golomba vārds. Solomons Golombs ir augsta līmeņa speciālists vairākās matemātikas nozarēs. Tomēr plašu popularitāti viņš ieguva tieši ar polimino. 1953. gadā, būdams Hārvarda Universitātes matemātikas nodaļas aspirants, Golombs nolasīja referātu par polimino. Uzskata, ka ar šo referātu arī aizsākās polimino vēsture.
Orientācija[labot šo sadaļu | labot pirmkodu]
- F, L, N, P un Y var būt orientēti 8 veidos: 4 pagriežot un 4 spoguļattēlā.
- T, U, V un W var būt orientēti 4 veidos pagriežot.
- Z var būt orientēts 4 veidos: 2 pagriežot un 2 spoguļattēlā.
- I var būt orientēts 2 veidos pagriežot.
- X var būt orientēts tikai vienā veidā.
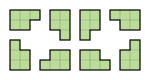
Piemēram, šīs ir visas 8 pentamino L, F, N, P and Y orientācijas:
Pentamino spēle[labot šo sadaļu | labot pirmkodu]
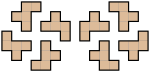
Ar "pentamino" bieži saprot spēli, kuras komplektā ietilpst 1. att. attēlotās figūras, un ar kurām jāveic "salikšanas" uzdevumi. Spēlētājam ir jāsaliek spēles pielikumā norādītās figūras. Ir iespējams, ka kādu no figūrām nemaz nav iespējams salikt.
Spēle Pentamino domāta vidējo un vecāko klašu skolēniem (citi Polimino varianti domāti bērniem vecumā no 8 līdz 14 gadiem). Tomēr šīs spēles varētu šķist interesantas arī vecākiem cilvēkiem.
No pentamino saliekami taisnstūri[labot šo sadaļu | labot pirmkodu]
Izmantojot pentamino komplektu, ir iespējams salikt jebkuru no taisnstūriem 3x20, 4x15, 5x12, 6x10.

Izmantošana[labot šo sadaļu | labot pirmkodu]
Ar ļoti sarežģītām matemātiskajām problēmām, kas saistītas ar polimino tematiku, nodarbojas augstas kvalifikācijas speciālisti, bet vienkāršākie polimino uzdevumi noder pat pirmskolas vecuma bērnu trenēšanā, kā arī viņu spēju noteikšanā. Polimino tēma ir piemērota fakultatīvām nodarbībām skolā, konkursu un olimpiāžu sastādītājiem un patstāvīgiem skolēnu pētījumiem. To var mācīt papildus skolas vielai.
Uzdevumu piemēri[labot šo sadaļu | labot pirmkodu]
- Vai eksistē figūra, kuru var salikt divos veidos no vieniem un tiem pašiem diviem pentamino?
- Vai eksistē divi pentamino, no kuriem var salikt tieši trīs simetriskus polimino?
- Vai eksistē figūra, kuru no vieniem un tiem pašiem trim pentamino var salikt trīs veidos?
- Vai pentamino I var sagriezt 4 daļās tā, lai no tām varētu salikt vienlielu kvadrātu?
- Atrast trīs pentamino, kurus var sagriezt 3 daļās tā, lai no tām varētu salikt ar pentamino vienlielu kvadrātu.
- Cik maksimāli daudz pentamino Y var izvietot katrā no kastītēm: 3x20, 4x15, 5x12 un 6x10?
- Vai no divām vienādām sagatavēm — katras izmēri 6x6 — var "izlauzt" visus pentamino?
- Vai taisnstūri 5x10 var salikt no pentamino, neizmantojot P un Y?
- Salikt divus vienādus taisnstūrus 5x4, neizmantojot L.
- Pierādīt, ka no pentamino nevar salikt taisnstūrus 5x3, 5x5.
Atsauces[labot šo sadaļu | labot pirmkodu]
- Cibulis, Andrejs (2001), Pentamino