Rādiuss
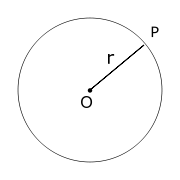
Par riņķa līnijas rādiusu sauc jebkuru nogriezni, kas savieno riņķa līnijas centru ar kādu no tās punktiem.[1] Par rādiusu mēdz saukt arī šī nogriežņa garumu. Riņķa līnijas un sfēras rādiuss ir vienāds ar pusi no tās diametra.
Vispārīgākā gadījumā ģeometrijā, grafu teorijā, inženierzinātnē un citās nozarēs rādiuss kādam objektam (piemēram, sfērai, cilindram, daudzstūrim, grafam) ir attālums no tā centra vai simetrijas ass līdz tā tālākajiem punktiem. Šādā gadījumā rādiuss var būt lielāks par pusi no diametra.
Lietojums[labot šo sadaļu | labot pirmkodu]
Visiem vienas riņķa līnijas rādiusiem ir vienāds garums, tāpēc riņķa līniju var viennozīmīgi uzdot, norādot tās rādiusu un centra koordinātas. Piemēram, ja riņķa līnijas rādiuss ir r un tās centrs ir punktā (x0, y0), tad šo riņķa līniju apraksta vienādojums
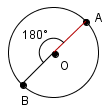
Divi viena riņķa rādiusi OA un OB, kas novietoti uz vienas taisnes (viens pret otru 180 grādu leņķī), veido šī riņķa diametru AB. Tātad, ja riņķa līnijas rādiuss ir r, tad tās diametrs ir
Rādiusu izmanto arī riņķa līnijas garuma un riņķa laukuma aprēķināšanai. Ja riņķa līnijas rādiuss ir r, tad tās garums ir
bet tai atbilstošā riņķa laukums ir
Skatīt arī[labot šo sadaļu | labot pirmkodu]
Atsauces[labot šo sadaļu | labot pirmkodu]
- ↑ Inese Lude, Jolanta Lapiņa. Matemātika 7. klasei. Pētergailis, 2013. 41. lpp.
Ārējās saites[labot šo sadaļu | labot pirmkodu]
- Encyclopædia Britannica raksts (angliski)
- Eric W. Weisstein, Radius, MathWorld.




