Ģeometrija


Ģeometrija (sengrieķu: γεωμετρία; geo - zeme, metria - mērīšana) ir matemātikas nozare, kurā tiek pētītas telpas īpašības, kā arī figūru izmērs, forma un savstarpējais novietojums. Ģeometrija ir viena no visvecākajām zinātnēm. Matemātiķi, kas nodarbojas ar ģeometriju, sauc par ģeometru.
Ģeometrija kā sistemātiska zinātne radās Senajā Grieķijā. 300. gadā p.m.ē. grieķis Eiklīds uzrakstīja darbu "Elementi", kas tiek uzskatīts par ģeometrijas pirmsākumu. Eiklīda ģeometrija nodarbojās ar plaknes un telpisku figūru izpēti, to laukuma un tilpuma aprēķināšanu. 1637. gada Dekarta piedāvātā koordinātu sistēma kļuva par analītiskās un diferenciālās ģeometrijas pamatu, bet uzdevumi, saistīti ar rasēšanu, noveda pie tēlotājas un projektīvās ģeometrijas veidošanās. 1829. gadā Lobačevskis atteicās no paralelitātes aksiomas un radīja jaunu neeiklīda ģeometriju, tādējādi nosakot turpmāko zinātnes attīstību un jaunu teorēmu izveidi.
1872. gadā Kleina piedāvātā ģeometrijas klasifikācija, kuras pamatā ir ģeometrisko objektu invariance, saglabājusies līdz šim.
Ģeometrijas apakšnozares[labot šo sadaļu | labot pirmkodu]
Ģeometrijas klasificēšana, ko piedāvāja Fēlikss Kleins savā "Erlangences programmā" (1872. gadā). Katra apakšnozare pēta konkrētas ģeometrisko objektu īpašības, kuras saglabājas, (invarianti) veicot dažus katrai nodaļai specifiskas pārveidojumu grupas. Pēc šīs klasifikācijas klasiskajā ģeometrijā var nodalīt galvenās apakšnozares.
- Eiklīda ģeometrija, kas paredz, ka, bīdot figūras plaknē, nogriežņu garumi un leņķu lielumi nemainās. Citiem vārdiem sakot, tā ir to figūru īpašību teorija, kuras paliek nemainīgas pie to pārbīdes, rotācijas, pagriešanas.
- Planimetrija — apskata figūras, kas atrodas vienā plaknē.
- Stereometrija — apskata figūras, kas atrodas trīsdimensiju telpā.
- Projektīvā ģeometrija — pēta īpašības, kas, projicējot figūru, paliek invariantas.
- Afīnā ģeometrija — pēta figūru īpašības, kuras paliek nemainīgas, veicot afīnos pārveidojumus.
- Tēlotāja ģeometrija — aplūko telpas objektu (punktu, līniju, virsmu un ķermeņu) attēlošanu plaknē. Šī metode izmanto divas vai vairākas projekcijas, kas ļauj attēlot telpiskus ķermeņus plaknē.
- Daudzdimensiju ģeometrija
- Diferenciālā ģeometrija — pēta līnijas un virsmas, izmanto diferenciāļa un atvasinājuma jēdzienus.
- Algebriskā ģeometrija — izmanto abstraktās algebras metodes.
- Analītiskā ģeometrija — ar algebras palīdzību pēta ģeometrisku objektu formu un īpašības. Tā balstās uz koordinātu metodi.
- Neeiklīda ģeometrijas — ģeometrijas, kurās neizpildās Eiklīda piektais (jeb paralēļu) postulāts:
- Sfēriskā ģeometrija
- Lobačevska ģeometrija
- Eliptiskā ģeometrija — ģeometrija uz virsmas ar pozitīvu liekuma rādiusu,
- Hiperboliskā ģeometrija — ģeometrija uz virsmas ar negatīvu liekuma rādiusu.
Aksiomas[labot šo sadaļu | labot pirmkodu]
Eiklīda ģeometrijas aksiomas, kuras tika formulētas III—IV gs. p.m.ē., kalpoja par ģeometrijas pamatu līdz XIX gs. otrai pusei, jo labi aprakstīja fizisko telpu.[1] Ar pieciem Eiklīda postulātiem bija par maz, lai pilnībā aprakstītu visu ģeometriju, un 1899. gadā Hilberts piedāvāja savu aksiomu sistēmu. Hilberts sadalīja aksiomas pa grupām: piederības, kongruences, nepartrauktības (tajā skaitā Arhimēda aksioma),pilnības un paralelitātes aksiomas. Vēlāk Šurs aizstāja kongruences aksiomas ar kustības aksiomuām, bet pilnības aksiomas vietā sāka lietot Kantora aksiomu. Ar Eiklīda ģeometrijas aksiomu sistēmas palīdzību ir iespējams pierādīt visas skolā pazīstamās teorēmas.[2]
Eksistē arī citas aksiomu sistēmas, kuru pamatā, neskaitot punktu, taisni un plakni, ir nevis kustība, bet kongruence, kā Hilbertam, vai attālums - kā Kaganam. Cita aksiomu sistēma saistīta ar vektoru jēdzienu. Visas viņas ir izvadītas viena no otras, tas ir - aksiomas no vienas sistēmas var pierādīt kā teorēmas no citas.[2]
Lai pierādītu to, ka Eiklīda ģeometrijas aksiomas nav pretrunā viena ar otru, un ir pilnīgas, tiek būvēts tas aritmētiskais modelis un rādīts, ka jebkurš modelis if izomorfs aritmētiskajam, kas nozīmē, ka tie ir izomorfi savā starpā.[3] Eiklīda ģeometrijas neatkarīgumu attēlot ir grūtāk, aksiomu lielā skaita dēļ. Paralelitātes aksioma nav atkarīga no citām, jo uz pretējā apgalvojuma balstās Lobačevska ģeometrija. Analoģiski tika pierādīta Arhimēda (trīs reālu skaitļu vietā tika paņemti trīs kompleksie skaitļi) un Kantora (par koordinātēm tika paņemti nevis trīs brīvi izvēlēti reāli skaitļi, bet tie tika noteiktā veidā iegūti) aksiomas kā arī viena no piederības aksiomām, kas faktiski nosaka telpas izmērus (jebkuras trīsdimensiju telpas vietā var uzbūvēt četru dimensiju telpu, bet jebkura daudzdimensiju telpa ir galīga).[4]
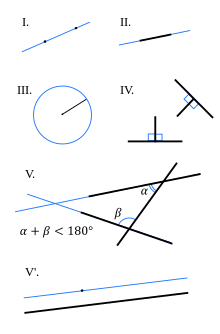
Eiklīda postulāti[labot šo sadaļu | labot pirmkodu]
Eiklīda postulāti ir konstruēšanas likumi, izmantojot ideālu cirkuli un ideālu lineālu [5]
- Divus punktus var savienot ar vienu vienīgu taisni.
- Taisnes nogriezni abos tā galos uz taisnes var pagarināt.
- Ap katru punktu kā ap centru var apvilkt riņķa līniju ar jebkādu rādiusu.
- Visi taisnie leņķi ir vienādi.
- Ja dotā plaknē ir taisne un punkts, kas neatrodas uz taisnes, tad caur šo punktu var novilkt vienu vienīgu taisni, kura nekrusto doto taisni.
Eiklīda ģeometrijas aksiomas[labot šo sadaļu | labot pirmkodu]
Elementārās matemātikas enciklopēdijā tiek piedāvāta sekojoša aksiomu sistēma[2]
- Piederības aksiomas
- Caur katriem diviem dažādiem punktiem var novilkt vienu vienīgu taisni;
- Uz katras taisnes atrodas vismaz divi dažādi punkti;
- Eksistē trīs punkti, kuri neatrodas uz vienas taisnes;
- Caur katriem trīs dažādiem punktiem, kas neatrodas uz vienas taisnes, var novilkt vienu vienīgu plakni;
- Katra plakne satur vismaz vienu punktu;
- Ja divi dažādi punkti atrodas uz vienas plaknes, tad arī novilktā caur šiem punktiem taisne atradīsies uz šīs plaknes;
- Ja divām plaknēm ir kopīgs punkts, tad tām ir vēl vismaz viens kopīgs punkts;
- Eksistē četri punkti, kas neatrodas vienā plaknē.
- Kārtības aksiomas:
- No jebkuriem trim dažādiem vienai taisnei piederošiem punktiem viens vienīgais to tiem atrodas starp pārējiem diviem;
- Jebkuriem diviem dažādiem vienai taisnei piederošiem punktiem var atrast trešo punktu, kas pieder šai taisnei, ka otrais punkts atradīsies starp pirmo un trešo;
- Ja taisne l, kas atrodas plaknē ABC, neiet ne caur vienu no punktiem A, B, C un satur vienu nogriežņa AB punktu, tad tā noteikti saturēs vienu no nogriežņa AC vai BC punktiem;
- Kustības aksiomas:
- Jebkura kustība ir savstarpēji nepārprotams telpas attēlojums uz sevi;
- f - patvaļīga kustība. Tad, ja punkti A, B, C atrodas uz vienas taisnes, pie tam C atrodas starp A un B, tad f(A), f(B), f(C) arī atradīsies uz vienas taisnes, pie tam f(C) atradīsies starp f(A) un f(B);
- Divas kustības, kas veiktas viena aiz otras ir līdzvērtīgas kādai vienai citai;
- Nepārtrauktības aksiomas:
- Arhimēda aksioma. A0, A1, B —trīs punkti, kas atrodas uz vienas taisnes, pie tam A1 atrodas starp A0 un B. f — kustība, kas pārveido punktu A0 punktā A1 un staru A0B starā A1B. Atliksim f(A1)=A2, f(A2)=A3, …. Tad eksistē tāds naturāls skaitlis n, ka punkts B atrodas uz nogriežņa An-1An.
- Kantora aksioma. A1, A2, … и B1, B2, … — tādas divas punktu sekvences, kas atrodas uz teisnes l, ka jebkuram n punkti An un Bn ir dažādi savā starpā un atrodas uz nogrižņa An-1Bn-1. Tad uz taisnes l eksistē tāds punkts C, kas atrodas uz nogrižņa AnBn pie jebkuras n vērtības.
- Paralelitātes aksioma:
- Caur punktu A, kas nepieder taisnei l, to plaknē var novilkt vienu vienīgu taisni, kas nekrustos taisni l.
Ģeometrijas pamatjēdzieni[labot šo sadaļu | labot pirmkodu]
Matemātikā par pamatjēdzieniem sauc jēdzienus, ko nedefinē. Parasti tiem dod tikai intuitīvu paskaidrojumu. Ģeometrijas pamatjēdzieni ir punkts, taisne un plakne.
- Punkts
- Intuitīvi punktu saprot kā 0-dimensionālu objektu (objektu, kam nav ne tilpuma, laukuma, ne garuma). Eiklīds punktu aprakstīja kā "tas, kam nav nekādu sastāvdaļu". Punkta atrašanās vietu telpā raksturo ar tā koordinātām. Punktus parasti apzīmē ar lielajiem burtiem A, B, C, ...
- Taisne
- Ģeometrijā ar taisni saprot bezgalīgu taisnu līniju. Taisne ir 1-dimensionāls objekts. Tā ir neierobežota uz abām pusēm, tāpēc zīmējumā var attēlot tikai taisnes daļu jeb nogriezni. Taisnes pieņemts apzīmēt ar mazajiem burtiem a, b, c, … vai arī ar diviem lielajiem burtiem, piemēram, AB, kur A un B ir divi atšķirīgi taisnes punkti.
- Plakne
- Plakni intuitīvi saprot kā bezgalīgu plakanu virsmu. Tā ir 2-dimensionāls objekts. Plakni var raksturot ar trīs tās punktiem, kas neatrodas uz vienas taisnes. Piemēram, plakne ABC.
Ģeometriskās figūras[labot šo sadaļu | labot pirmkodu]
- Stars
- Stars ir taisnes daļa uz vienu pusi no kāda taisnes punkta. Šo punktu sauc par sākumpunktu un parasti apzīmē ar O. Staru apzīmē ar tā sākumpunktu un vēl kādu punktu uz stara, piemēram, stars OT. Jebkurš taisnes punkts O to sadala divos staros, piemēram, OS un OT.
- Nogrieznis
- Par nogriezni sauc taisnes daļu starp diviem tās punktiem. Šos punktus sauc par nogriežņa galapunktiem. Nogriezni apzīmē ar tā galapunktiem vai ar vienu mazo burtu, piemēram, nogrieznis GH vai nogrieznis d. Ja viens nogrieznis ir otra nogriežņa daļa, tad saka, ka otrais nogrieznis ir lielāks nekā pirmais, pieraksta, AB > CD.
- Trīsstūris
- Trijstūris ir ģeometriska figūra, ko veido trīs punkti un taisnes nogriežņi. Trijstūri ar virsotnēm A, B un C apzīmē ar . Eiklīda ģeometrijā trijstūri veido jebkuri trīs savā starpā nekolineāri punkti. Arī neeiklīda ģeometrijās trijstūrim ir tāda pati nozīme, tomēr tam tajās ir specifiskas īpašības.
- Kvadrāts
- Kvadrāts jeb regulārs četrstūris ir četrstūris, kuram visas malas ir vienāda garuma un visi leņķi ir vienādi, un ir 90 grādi. Kvadrātu var uzskatīt par taisnstūri, kuram visas malas ir vienādas, vai arī par rombu, kuram leņķi ir 90 grādi. Kvadrātam, tāpat kā jebkuram četrstūrim, ir divas diagonāles.
- Riņķa līnija
- Riņķa līnija ir visu to plaknes punktu kopa, kuri atrodas vienādā attālumā no kāda fiksēta plaknes punkta. Šo punktu sauc par riņķa līnijas centru, bet attālumu — par tās rādiusu. Riņķa līnijas un riņķa jēdzieni ir cieši saistīti, taču nav identiski. Riņķis ir riņķa līnijas iekšpuse jeb plaknes daļa, ko ierobežo riņķa līnija un kurā atrodas tās centrs.
Atsauces[labot šo sadaļu | labot pirmkodu]
- ↑ Геометрия // Математическая энциклопедия : в 5 т.. — М. : Советская Энциклопедия, 1982. — Т. 1
- ↑ 2,0 2,1 2,2 Геометрия, 1963, с. 32—41
- ↑ Геометрия, 1963, с. 41—44.
- ↑ Геометрия, 1963, с. 44—48.
- ↑ Геометрия, 1963, с. 12—17
Ārējās saites[labot šo sadaļu | labot pirmkodu]
 Vikikrātuvē par šo tēmu ir pieejami multivides faili. Skatīt: Ģeometrija.
Vikikrātuvē par šo tēmu ir pieejami multivides faili. Skatīt: Ģeometrija.
- Encyclopædia Britannica raksts (angliski)
- Mūsdienu Ukrainas enciklopēdijas raksts (ukrainiski)
- Krievijas Lielās enciklopēdijas raksts (krieviski)
- Encyclopædia Universalis raksts (franciski)
- Enciklopēdijas Krugosvet raksts (krieviski)
- Eric W. Weisstein, Geometry, MathWorld.
- David Eppstein, The Geometry Junkyard.
- Karīna Oborune, Vai vēlies nopelnīt miljonu? Studē ģeometriju!, Universitātes Avīze, 2008. gada 17. aprīlis.
| Šis ar matemātiku saistītais raksts ir nepilnīgs. Jūs varat dot savu ieguldījumu Vikipēdijā, papildinot to. |
|

