Kvadrātnevienādība
Ir ierosināts pārvietot šo lapu uz Wikibooks. Ja šo lapu var pārrakstīt tā, lai tā iederētos enciklopēdijā, lūdzu, izdari tā un noņem šo paziņojumu. Pirms pārvietošanas uz Wikibooks pārliecinies, ka šī lapa tur iederēsies (skatīt What is Wikibooks? angliski). Bieži vien saturs, kas neiederas Vikipēdijā, neiederas arī citos projektos. |
Nevienādības, kuras vispārīgais veids ir (<0, ≤0, ≥0), kur a, b,c ∈ un a≠0, bet ir mainīgais, sauc par kvadrātnevienādību.[1]
Kvadrātnevienādību iedalījums[2]
[labot šo sadaļu | labot pirmkodu]Kvadrātnevienādības iedala tāpat kā lineārās nevienādības.
Stingrās kvadrātnevienādības
[labot šo sadaļu | labot pirmkodu]Par stingrām kvadrātnevienādībām sauc kvadrātnevienādības, kuras satur zīmi vai .
Nestingrās kvadrātnevienādības
[labot šo sadaļu | labot pirmkodu]Par nestingrām kvadrātnevienādībām, sauc kvadrātnevienādības, kuras satur zīmi vai .
Pilnās kvadrātnevienādības[3]
[labot šo sadaļu | labot pirmkodu]Par pilnām kvadrātnevienādībām sauc kvadrātnevienādības, kur visi trīs koeficienti , un ir no nulles atšķirīgi skaitļi.
Nepilnās kvadrātnevienādības
[labot šo sadaļu | labot pirmkodu]Par nepilnām kvadrātnevienādībām sauc kvadrātnevienādības, kurās kaut viens no koeficientiem vai ir vienāds ar nulli.
Kvadrātnevienādības risinājums
[labot šo sadaļu | labot pirmkodu]

Atrisināt nevienādību nozīmē atrast visus tās atrisinājumus (norādīt atrisinājuma intervālu) un pierādīt, ka nevienādībai citu atrisinājumu nav.
Nosaka parabolas krustpunktus ar asi (atrod funkcijas nulles), atrisinot vienādojumu .
[labot šo sadaļu | labot pirmkodu]Izmanto kvadrātvienādojuma formulas:[4]
- Ja , tad vienādojumam ir divas dažādas saknes, parabola krusto asi divos punktos.
- Ja , tad vienādojumam ir divas vienādas saknes, parabolas virsotne atrodas uz ass.
- Ja , tad vienādojumam nav reālu sakņu, parabola asi nekrusto.
Kvadrātvienādojuma saknes var aprēķināt arī izmantojot Vjeta teorēmu.
Ņemot vērā sakņu skaitu un koeficienta zīmi, skicē parabolas grafiku.
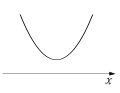
[labot šo sadaļu | labot pirmkodu]- Ja , tad zari vērsti uz augšu.
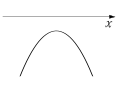
- Ja , tad zari vērsti uz leju.
Izvēlās tukšus vai pildītus punktus, atkarībā no nevienādības zīmes.
[labot šo sadaļu | labot pirmkodu]- Tukšs, ja kvadrātnevienādība satur zīmes vai .
- Pildīts, ja kvadrātnevienādība satur zīmes vai .
Pēc parabolas grafika nosaka kvadrātnevienādības atrisinājumu.
[labot šo sadaļu | labot pirmkodu]-
Parabola nekrusto asi.
-
Parabola nekrusto asi.
-
Parabolas virsotne atrodas uz ass.
Skatīt arī
[labot šo sadaļu | labot pirmkodu]Ārējās saites
[labot šo sadaļu | labot pirmkodu]Atsauces
[labot šo sadaļu | labot pirmkodu]- ↑ "Matemātika 9.klasei", Ilze France, Gunta Lāce, Ligita Packaine, Anita Miķelsone, 87.lpp
- ↑ "Matemātika 11.klasei", Evija Slokenberga, Inga France, Ilze France, 7. lpp
- ↑ "Matemātika 8.klasei", Ilze France, Gunta Lāce, Ligita Pickaine, Anita Miķelsone, 108.lpp
- ↑ "Quadratic Equation" From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/QuadraticEquation.html, Weisstein, Eric W