Divkāršais integrālis ir noteiktā integrāļa vispārinājums, kad integrēšanas apgabals D ir plaknes apgabals, bet zemintegrāļa funkcija ir divu argumentu funkcija z = f(x, y). Divkāršo integrāli apzīmē ar simbolu
∬
(
D
)
f
(
x
,
y
)
d
S
.
{\displaystyle \iint \limits _{(D)}f(x,y)dS.}
[ 1]
Ja
f
(
x
,
y
)
⩾
0
{\displaystyle f(x,y)\geqslant 0}
tilpumu V , ko ierobežo funkcijas z = f(x, y) grafiks (tas ir, virsma ar vienādojumu z = f(x, y) ), xy plaknes apgabals (D ) un cilindriska virsma ar veidotājām paralēlām Oz asij, kas iet caur apgabala (D ) robežlīniju. Tātad
∬
(
D
)
f
(
x
,
y
)
d
S
=
V
.
{\displaystyle \iint \limits _{(D)}f(x,y)dS=V.}
[ 2]
Pieņem, ka funkcija z = f(x, y) ir definēta Oxy apgabalā (D ):
Ar brīvi izraudzītām līnijām apgabalu (D ) sadala n daļās (D1 ), (D2 ), (D3 ), ..., (Di ), ..., (Dn ). Šo daļu laukumus apzīmē ar
△
S
1
,
△
S
2
,
△
S
3
,
.
.
.
,
△
S
i
,
.
.
.
,
△
S
n
.
{\displaystyle \bigtriangleup S_{1},\bigtriangleup S_{2},\bigtriangleup S_{3},...,\bigtriangleup S_{i},...,\bigtriangleup S_{n}.}
Katrā apgabala daļā (Di ) brīvi izraugās punktu
M
i
(
ξ
i
;
η
i
)
∈
(
D
i
)
{\displaystyle M_{i}(\xi _{i};\eta _{i})\in (D_{i})}
1
⩽
i
⩽
n
{\displaystyle 1\leqslant i\leqslant n}
Aprēķina funkcijas z = f(x, y) vērtības izraudzītajos punktos, tas ir, atrod
f
(
M
i
)
=
f
(
ξ
i
;
η
i
)
{\displaystyle f(M_{i})=f(\xi _{i};\eta _{i})}
1
⩽
i
⩽
n
{\displaystyle 1\leqslant i\leqslant n}
Atrastās funkcijas vērtības
f
(
ξ
i
;
η
i
)
{\displaystyle f(\xi _{i};\eta _{i})}
reizina ar tās apgabala daļas (Di ) laukumu
△
S
i
{\displaystyle \bigtriangleup S_{i}}
M
i
{\displaystyle M_{i}}
f
(
ξ
i
;
η
i
)
{\displaystyle f(\xi _{i};\eta _{i})}
△
S
i
{\displaystyle \bigtriangleup S_{i}}
1
⩽
i
⩽
n
{\displaystyle 1\leqslant i\leqslant n}
Aprēķina visu reizinājumu
f
(
ξ
i
;
η
i
)
{\displaystyle f(\xi _{i};\eta _{i})}
△
S
i
{\displaystyle \bigtriangleup S_{i}}
∑
i
=
1
n
f
(
ξ
i
;
η
i
)
△
S
i
.
{\displaystyle \sum _{i=1}^{n}f(\xi _{i};\eta _{i})\bigtriangleup S_{i}.}
z = f(x, y) integrālsummu apgabalā (D) .
Aprēķina integrālsummas robežu , kad maksimālais apgabala daļas (Di ) diametrs di tiecas uz 0 (par daļas (Di ) diametru sauc taisnes nogriezni , kas savieno divus vistālākos (Di ) robežlīnijas punktus), tas ir aprēķina
lim
d
→
0
∑
i
=
1
n
f
(
ξ
i
;
η
i
)
△
S
i
.
{\displaystyle \lim _{d\to 0}\sum _{i=1}^{n}f(\xi _{i};\eta _{i})\bigtriangleup S_{i}.}
Ja šī robeža eksistē neatkarīgi no dalījuma veida daļās un no punktu izvēles katrā daļā, tad šo robežu sauc par funkcijas z = f(x, y) divkāršo integrāli apgabalā (D ) un apzīmē ar simbolu
∬
(
D
)
f
(
x
,
y
)
d
S
{\displaystyle \iint \limits _{(D)}f(x,y)dS}
[ 2]
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
.
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy.}
[ 3]
Tādējādi
lim
d
→
0
∑
i
=
1
n
f
(
ξ
i
;
η
i
)
△
S
i
=
∬
(
D
)
f
(
x
,
y
)
d
S
.
{\displaystyle \lim _{d\to 0}\sum _{i=1}^{n}f(\xi _{i};\eta _{i})\bigtriangleup S_{i}=\iint \limits _{(D)}f(x,y)dS.}
[ 2]
Ja funkcija z = f(x, y) apgabalā (D ) ir nepārtraukta vai gabaliem pārtraukta, tad šai funkcijai eksistē divkāršais integrālis.[ 2]
Divkāršais integrālis no funkcijas summas (starpības ) ir vienāds ar doto funkciju integrāļu summu (starpību):
∬
(
D
)
(
f
1
(
x
,
y
)
+
f
1
(
x
,
y
)
)
d
x
d
y
=
∫
(
D
)
f
1
(
x
,
y
)
d
x
d
y
+
∫
(
D
)
f
2
(
x
,
y
)
d
x
d
y
+
.
.
.
+
∫
(
D
)
f
n
(
x
,
y
)
d
x
d
y
.
{\displaystyle \iint \limits _{(D)}(f_{1}(x,y)+f_{1}(x,y))dxdy=\int \limits _{(D)}f_{1}(x,y)dxdy+\int \limits _{(D)}f_{2}(x,y)dxdy+...+\int \limits _{(D)}f_{n}(x,y)dxdy.}
[ 3]
Konstantu reizinātāju C var ņemt pirms integrāļa zīmes:
∬
(
D
)
C
f
(
x
,
y
)
d
x
d
y
=
C
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
.
{\displaystyle \iint \limits _{(D)}Cf(x,y)dxdy=C\iint \limits _{(D)}f(x,y)dxdy.}
[ 3]
Ja apgabals (D) sadalīts vairākās daļās, tad integrē pa katru daļu atsevišķi un iegūtos rezultātus saskaita:
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
=
∫
(
D
1
)
f
(
x
,
y
)
d
x
d
y
+
∫
(
D
2
)
f
(
x
,
y
)
d
x
d
y
+
.
.
.
+
∫
(
D
n
)
f
(
x
,
y
)
d
x
d
y
.
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy=\int \limits _{(D_{1})}f(x,y)dxdy+\int \limits _{(D_{2})}f(x,y)dxdy+...+\int \limits _{(D_{n})}f(x,y)dxdy.}
[ 3]
Ja apgabalā (D) funkcija saglabā zīmi
f
(
x
,
y
)
⩾
0
{\displaystyle f(x,y)\geqslant 0}
(
⩽
0
)
{\displaystyle (\leqslant 0)}
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
⩾
0
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy\geqslant 0}
(
⩽
0
)
.
{\displaystyle (\leqslant 0).}
[ 3]
Ja apgabalā (D) visiem (x, y ) izpildās nevienādība
f
(
x
,
y
)
⩽
g
(
x
,
y
)
{\displaystyle f(x,y)\leqslant g(x,y)}
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
⩽
∬
(
D
)
g
(
x
,
y
)
d
x
d
y
.
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy\leqslant \iint \limits _{(D)}g(x,y)dxdy.}
[ 3]
Ja funkcijai z = f(x, y) slēgtā apgabalā (D ) ir nepārtraukta un m ir funkcijas z = f(x, y) vismazākā vērtība, bet M ir funkcijas z = f(x, y) vislielākā vērtība apgabalā (D), tas ir,
m
⩽
f
(
x
,
y
)
⩽
M
{\displaystyle m\leqslant f(x,y)\leqslant M}
m
S
⩽
∬
(
D
)
g
(
x
,
y
)
d
x
d
y
⩽
M
S
,
{\displaystyle mS\leqslant \iint \limits _{(D)}g(x,y)dxdy\leqslant MS,}
kur S ir apgabala (D ) laukums.[ 3]
Ja funkcija z = f(x, y) slēgtā apgabalā (D ) ir nepārtraukta, tad apgabalā (D ) eksistē vismaz viens tāds punkts P , ka divkāršais integrālis pa apgabalu (D ) ir vienāds ar zemintegrāļa funkcijas vērtību šajā punktā, reizinātu ar apgabala (D ) laukumu S :
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
=
f
(
P
)
⋅
S
.
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy=f(P)\centerdot S.}
Funkcijas z = f(x, y) vērtību
f
(
P
)
{\displaystyle f(P)}
integrālo vidējo vērtību apgabalā (D ).[ 3]
Apgabalu (D ) sauc par regulāru Oy ass virzienā , ja jebkura taisne, kas paralēla Oy asij, šī apgabala robežu krusto ne vairāk kā divos
punktos.
Apgabalu (D ) sauc par regulāru Ox ass virzienā , ja jebkura taisne, kas paralēla Ox asij, šī apgabala robežu krusto ne vairāk kā divos punktos.[ 3]
Divkāršo integrāli Dekarta koordinātu sistēmā reducē uz atkārtotiem integrāļiem . Tos var pierakstīt divos veidos pēc tā, kādā virzienā apgabals (D ) ir pareizs:
I
1
=
∫
a
b
d
x
∫
y
1
(
x
)
y
2
(
x
)
f
(
x
,
y
)
d
y
{\displaystyle I_{1}=\int \limits _{a}^{b}dx\int \limits _{y_{1}(x)}^{y_{2}(x)}f(x,y)dy}
Oy ass virzienā)
un
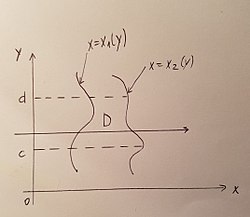
I
2
=
∫
c
d
d
y
∫
x
1
(
y
)
x
2
(
y
)
f
(
x
,
y
)
d
x
{\displaystyle I_{2}=\int \limits _{c}^{d}dy\int \limits _{x_{1}(y)}^{x_{2}(y)}f(x,y)dx}
Ox ass virzienā).[ 3]
Ārējās integrāļa robežas vienmēr ir konstantas.[ 3]
Ja apgabals nav pareizs ne Oy, ne Ox ass virzienā, tad apgabalu (D ) sadala atsevišķā daļās, integrē pa katru daļu atsevišķi un iegūtos rezultātus saskaita.
Atkārtotos integrāļus aprēķina šādi:
I
1
=
∫
a
b
d
x
∫
y
1
(
x
)
y
2
(
x
)
f
(
x
,
y
)
d
y
=
∫
a
b
(
∫
y
1
(
x
)
y
2
(
x
)
f
(
x
,
y
)
d
y
)
d
x
=
∫
a
b
F
1
(
x
,
y
)
|
y
=
y
1
(
x
)
y
=
y
2
(
x
)
d
x
=
∫
a
b
(
F
1
(
x
,
y
2
(
x
)
)
−
F
1
(
x
,
y
1
(
x
)
)
)
d
x
=
ϕ
1
(
x
)
|
a
b
=
ϕ
1
(
b
)
−
ϕ
1
(
a
)
=
K
1
{\displaystyle I_{1}=\int \limits _{a}^{b}dx\int \limits _{y_{1}(x)}^{y_{2}(x)}f(x,y)dy=\int \limits _{a}^{b}{\biggl (}\int \limits _{y_{1}(x)}^{y_{2}(x)}f(x,y)dy{\biggr )}dx=\int \limits _{a}^{b}F_{1}(x,y)|_{y=y_{1}(x)}^{y=y_{2}(x)}dx=\int \limits _{a}^{b}{\Biggl (}F_{1}(x,y_{2}(x))-F_{1}(x,y_{1}(x)){\Biggr )}dx=\phi _{1}(x)|_{a}^{b}=\phi _{1}(b)-\phi _{1}(a)=K_{1}}
y , bet mainīgo x uzskata par konstanti)
un
I
2
=
∫
c
d
d
y
∫
x
1
(
y
)
x
2
(
y
)
f
(
x
,
y
)
d
x
=
∫
c
d
(
∫
x
1
(
y
)
x
2
(
y
)
f
(
x
,
y
)
d
x
)
d
y
=
∫
c
d
F
2
(
x
,
y
)
|
x
=
x
1
(
y
)
x
=
x
2
(
y
)
d
y
=
∫
c
d
(
F
2
(
x
2
(
y
)
,
y
)
−
F
2
(
x
1
(
y
)
)
d
x
=
ϕ
2
(
y
)
|
c
d
=
ϕ
2
(
d
)
−
ϕ
2
(
c
)
=
K
2
{\displaystyle I_{2}=\int \limits _{c}^{d}dy\int \limits _{x_{1}(y)}^{x_{2}(y)}f(x,y)dx=\int \limits _{c}^{d}{\biggl (}\int \limits _{x_{1}(y)}^{x_{2}(y)}f(x,y)dx{\biggr )}dy=\int \limits _{c}^{d}F_{2}(x,y)|_{x=x_{1}(y)}^{x=x_{2}(y)}dy=\int \limits _{c}^{d}{\Biggl (}F_{2}(x_{2}(y),y)-F_{2}(x_{1}(y){\Biggr )}dx=\phi _{2}(y)|_{c}^{d}=\phi _{2}(d)-\phi _{2}(c)=K_{2}}
(iekšējo integrāli rēķina pēc x, bet mainīgo y uzskata par konstanti).[ 3]
Divkāršā integrāļa aprēķināšanu var vienkāršot, ieviešot jaunus mainīgos (u, v ) ar formulām:
{
x
=
x
(
u
,
v
)
;
y
=
y
(
u
,
v
)
.
{\displaystyle {\begin{cases}x=x(u,v);\\y=y(u,v).\end{cases}}}
Iegūst:
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
=
∬
(
D
)
f
(
x
(
u
,
v
)
,
y
(
u
,
v
)
)
|
J
(
u
,
v
)
|
d
u
d
v
,
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy=\iint \limits _{(D)}f(x(u,v),y(u,v))|J(u,v)|dudv,}
kur
J
(
u
,
v
)
{\displaystyle J(u,v)}
Jakobi determinants jakobiāns :
J
(
u
,
v
)
=
|
∂
x
∂
u
∂
x
∂
v
∂
y
∂
u
∂
y
∂
v
|
.
{\displaystyle J(u,v)={\begin{vmatrix}{\partial x \over \partial u}&{\partial x \over \partial v}\\{\partial y \over \partial u}&{\partial y \over \partial v}\end{vmatrix}}.}
[ 3]
Polārās un Dekarta koordinātas Ja integrācijas apgabalu (D ) ierobežo riņķa līnijas vai arī līniju vienādojumi un zemintegrāļa izteiksme satur kvadrātu summu
x
2
+
y
2
{\displaystyle x^{2}+y^{2}}
polārajām koordinātām
(
φ
,
r
)
{\displaystyle (\varphi ,r)}
{
x
=
r
c
o
s
φ
;
y
=
r
s
i
n
φ
.
⟹
x
2
+
y
2
=
r
2
{\displaystyle {\begin{cases}x=rcos\varphi ;\\y=rsin\varphi .\end{cases}}\Longrightarrow x^{2}+y^{2}=r^{2}}
Jakobiānu aprēķina pēc formulas:
J
(
u
,
v
)
=
|
∂
x
∂
u
∂
x
∂
v
∂
y
∂
u
∂
y
∂
v
|
=
|
c
o
s
φ
−
r
s
i
n
φ
s
i
n
φ
r
c
o
s
φ
|
=
r
.
{\displaystyle J(u,v)={\begin{vmatrix}{\partial x \over \partial u}&{\partial x \over \partial v}\\{\partial y \over \partial u}&{\partial y \over \partial v}\end{vmatrix}}={\begin{vmatrix}cos\varphi &-rsin\varphi \\sin\varphi &rcos\varphi \end{vmatrix}}=r.}
[ 3]
Iegūst pārejas formulu no Dekarta uz polārajām koordinātām:
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
=
∬
(
D
)
f
(
r
c
o
s
φ
,
r
s
i
n
φ
)
r
d
r
d
φ
.
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy=\iint \limits _{(D)}f(rcos\varphi ,rsin\varphi )rdrd\varphi .}
Ja plaknes apgabalu ierobežo stari
φ
=
α
;
φ
=
β
{\displaystyle \varphi =\alpha ;\varphi =\beta }
r
=
r
1
(
φ
)
;
r
=
r
2
(
φ
)
{\displaystyle r=r_{1}(\varphi );r=r_{2}(\varphi )}
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
=
∫
α
β
d
φ
∫
r
1
(
φ
)
r
2
(
φ
)
f
(
r
c
o
s
φ
,
r
s
i
n
φ
)
r
d
r
.
{\displaystyle \iint \limits _{(D)}f(x,y)dxdy=\int \limits _{\alpha }^{\beta }d\varphi \int \limits _{r_{1}(\varphi )}^{r_{2}(\varphi )}f(rcos\varphi ,rsin\varphi )rdr.}
[ 3]
Ja zemintegrāļa funkcija
f
(
x
,
y
)
=
1
{\displaystyle f(x,y)=1}
D ) laukumu Dekarta un polārajās koordinātās:
S
=
∬
(
D
)
d
S
=
∬
(
D
)
d
x
d
y
=
∬
(
D
)
r
d
r
d
φ
.
{\displaystyle S=\iint \limits _{(D)}dS=\iint \limits _{(D)}dxdy=\iint \limits _{(D)}rdrd\varphi .}
[ 1] [ 3]
Ķermeni ierobežo funkcijas
z
=
f
1
(
x
,
y
)
,
z
=
f
2
(
x
,
y
)
{\displaystyle z=f_{1}(x,y),z=f_{2}(x,y)}
Ja ķermeni ierobežo funkcijas
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
f
(
x
,
y
)
⩾
0
{\displaystyle f(x,y)\geqslant 0}
Oxy plakne un Oz asij paralēla cilindriska virsma, kas iet caur apgabala (D ) robežlīniju. Šāda ķermeņa tilpums ir vienāds ar
V
=
∬
(
D
)
f
(
x
,
y
)
d
x
d
y
.
{\displaystyle V=\iint \limits _{(D)}f(x,y)dxdy.}
[ 1]
Ja ķermeni ierobežo Oz asij paralēla cilindriska virsma, kas iet caur apgabala (D ) robežlīniju un divu funkciju
z
=
f
1
(
x
,
y
)
,
z
=
f
2
(
x
,
y
)
{\displaystyle z=f_{1}(x,y),z=f_{2}(x,y)}
0
⩽
f
1
(
x
,
y
)
⩽
f
2
(
x
,
y
)
{\displaystyle 0\leqslant f_{1}(x,y)\leqslant f_{2}(x,y)}
V
=
∬
(
D
)
(
f
2
(
x
,
y
)
−
f
1
(
x
,
y
)
)
d
x
d
y
.
{\displaystyle V=\iint \limits _{(D)}(f_{2}(x,y)-f_{1}(x,y))dxdy.}
[ 1]
Ja dota virsma
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
D ) — virsmas
z
=
f
(
x
,
y
)
{\displaystyle z=f(x,y)}
Oxy plaknē — un tai eksistē nepārtraukti parciālie atvasinājumi
z
x
′
{\displaystyle z'_{x}}
z
y
′
{\displaystyle z'_{y}}
S
=
∬
(
D
)
1
+
(
z
x
′
)
2
+
(
z
y
′
)
2
d
x
d
y
.
{\displaystyle S=\iint \limits _{(D)}{\sqrt {1+(z'_{x})^{2}+(z'_{y})^{2}}}dxdy.}
[ 1]
Ja nepārtraukta funkcija
ρ
(
x
,
y
)
{\displaystyle \rho (x,y)}
nehomogēnas plakanas plāksnītes (D ) virsmas blīvuma sadalījums, tad plāksnītes masa ir
m
=
∬
(
D
)
ρ
(
x
,
y
)
d
x
d
y
.
{\displaystyle m=\iint \limits _{(D)}\rho (x,y)dxdy.}
[ 1]
↑ 1,0 1,1 1,2 1,3 1,4 1,5 Inta Volodko. Augstākā matemātika II. Rīga : Zvaigzne ABC , 2009. 123.—135. lpp. ISBN 978-9984-40649-7 . ↑ 2,0 2,1 2,2 2,3 Kārlis Šteiners. Augstākā matemātika V. Rīga : Zvaigzne ABC , 2000. 7. lpp. ISBN 9984-17-930-3 . ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 3,12 3,13 3,14 3,15 V. Barkāns. Vairākargumentu funkciju integrāļi . Rīga : Latvijas Jūras akadēmija , 2010. 5.—16. lpp.