Bernulli likums

Bernulli likums ir fizikas likums hidrodinamikā, kas atspoguļo fluīda (šķidruma vai gāzes) ātruma, statiskā spiediena un potenciālās enerģijas savstarpējo saistību. Tas nosaka, ka kāds no šiem lielumiem var palielināties tikai tad, ja kāds cits no tiem samazinās.[1] Princips nosaukts Dāniela Bernulli vārdā, kurš to publicēja savā grāmatā Hydrodynamica 1738. gadā.[2] Lai arī Bernulli pirmais izsprieda, ka, palielinoties plūsmas ātrumam, samazinās spiediens, Bernulli vienādojumu mūsdienu formā pirmais ieguva Leonards Eilers 1752. gadā.[3][4] Šis likums ir piemērojams tikai izentropiskām (adiabātiskām un atgriezeniskām) plūsmām — tādām, kurās neatgriezeniski procesi un enerģijas apmaiņa ar ārējo vidi rada gana nelielu iespaidu, lai to neņemtu vērā.
Bernulli vienādojums nesaspiežamām plūsmām
[labot šo sadaļu | labot pirmkodu]Lielākajā daļā šķidrumu un gāzu plūsmu ar mazu Maha skaitli fluīda blīvumu var uzskatīt par konstantu neatkarīgi no spiediena atšķirībām plūsmā. Tāpēc šķidrumu šādās plūsmās var uzskatīt par nesaspiežamu, un šīs plūsmas sauc par nesaspiežamām plūsmām. Bieži Bernulli vienādojumu patvaļīgam nesaspiežamas plūsmas punktam raksta šādā formā:
,
kur:
- ir šķidruma plūsmas ātrums aplūkojamajā punktā,
- ir brīvās krišanas paātrinājums,
- ir punkta augstums virs atskaites līmeņa, vērtība pieaug virzienā uz augšu: pretēji gravitācijas virzienam,
- ir spiediens izvēlētajā punktā, un
- ir šķidruma blīvums visos šķidruma punktos.
Vienādojuma konstantā labās puses vērtība ir atkarīga tikai no izvēlētās plūsmas un ir tā pati jebkuram plūsmas punktam. Savukārt lielumu , un vērtības var būt atšķirīgas dažādos šīs plūsmas punktos.
Bernulli vienādojuma izvedums
[labot šo sadaļu | labot pirmkodu]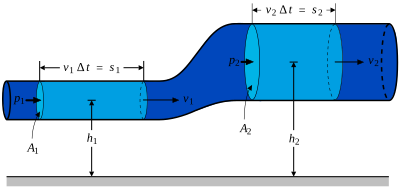
Bernulli vienādojumu nesaspiežamām plūsmām var iegūt, izmantojot enerģijas nezūdamības likumu. Mehāniskās enerģijas izmaiņu noteiktā laika posmā rada spiedienu un veiktais darbs, t.i.
,
kur — spiediena padarītais darbs laikā .
Nesaspiežamas plūsmas gadījumā laika sprīdī caurulē ieplūst tikpat liels šķidruma daudzums, cik izplūst pa otru galu. Apzīmēsim šī šķidruma masu ar un tilpumu ar .
Šķidruma kinētiskās un potenciālās enerģijas starpības iegūstam, no beigu enerģijas atņemot sākotnējo:
;
.
Spiediens ir spēka virsmai perpendikulārās komponentes attiecība pret laukumu, uz kuru šis spēks darbojas: . No spiediena nemainības stacionāras plūsmas noteiktā punktā izriet, ka arī spēka virsmai normālā (perpendikulārā) komponente tur ir nemainīga. Laukums izraudzīts tā, ka plūsmas pārvietojums ir tai perpendikulārs, tātad kolineārs spēkam . Darbu tad varam atrast kā spēka un pārvietojuma reizinājumu.
.
Vienādojumā saliekot uzieto, iegūstam (ievērojiet, ka otrā spiediena veiktais darbs ir negatīvs, jo šis spiediens darbojas pretim plūsmai):
Nogādāsim ar vienu punktu saistītos lielumus vienā, bet pārējos — otrajā vienādības pusē, kā arī izdalīsim abas vienādojuma puses ar . Papildus atminoties blīvuma definīciju esam ieguvuši:
.
Tātad, izteiksmes vērtība dažādās plūsmas vietās ir viena un tā pati, kas arī ir Bernulli likums.
Skatīt arī
[labot šo sadaļu | labot pirmkodu]- Hidraulika - šķidrumu mehānikas pielietojumi
- Hidroaeromehānika
Atsauces
[labot šo sadaļu | labot pirmkodu]- ↑ Visvaldis Branka, Valdis Gaumigs, Pēteris Puķītis. FIZIKA VIDUSSKOLAI. Konspektīvs izklāsts. Apgāds Zvaigzne ABC, 2007. 72–76. lpp. ISBN 978-9984-37-377-5.
- ↑ «Hydrodynamica». Britannica Online Encyclopedia. Skatīts: 2008-10-30.
- ↑ Anderson, J.D. (2016), "Some reflections on the history of fluid dynamics", in Johnson, R.W., Handbook of fluid dynamics (2nd izd.), CRC Press, ISBN 9781439849576
- ↑ Darrigol, O.; Frisch, U. (2008), "From Newton's mechanics to Euler's equations", Physica D: Nonlinear Phenomena 237 (14–17): 1855–1869, doi:10.1016/j.physd.2007.08.003
Ārējās saites
[labot šo sadaļu | labot pirmkodu] Vikikrātuvē par šo tēmu ir pieejami multivides faili. Skatīt: Bernulli likums.
Vikikrātuvē par šo tēmu ir pieejami multivides faili. Skatīt: Bernulli likums.
- Encyclopædia Britannica raksts (angliski)































