Trapece

Trapece ir tāds četrstūris, kam divas malas ir savstarpēji paralēlas, bet atlikušās divas nav savstarpēji paralēlas (attēlā redzama trapece $ABCD$ ).

Paralēlās malas sauc par trapeces pamatiem un parasti zīmē kā trapeces augšējo un apakšējo malu. Attiecīgi abas pārējās malas sauc par trapeces sānu malām jeb sāniem.

Trapeces augstums ir attālums starp tās pamatiem (attēlā: $BM$ un $CN$ )

Trapeces viduslīnija ir nogrieznis, kas savieno trapeces sānu malu viduspunktus (attēlā: $KL$ ). Jebkuras trapeces viduslīnija ir paralēla tās pamatiem.

Formulas

Trapeces laukumu $S$ var aprēķināt, zinot tās pamatu garumus un augstumu: $S={\frac {a+b}{2}}\cdot h$ .

Trapeces viduslīnija ( $KL$ ) ir paralēla pamatiem un tās garums ir: $KL={\frac {a+b}{2}}$ .

Trapeces laukumu iespējams izteikt arī ar viduslīniju: $S=KL\cdot h$

Īpašie gadījumi

Vienādsānu trapece

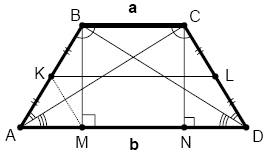
Vienādsānu trapece ir trapece, kuras sānu malas ir vienāda garuma (attēlā malas $AB$ un $CD$ ).

Vienādsānu trapecē ir vairāki vienādi un līdzīgi trijstūri, tāpēc tai piemīt vairākas papildu īpašības, kas nepiemīt patvaļīgai trapecei.

Trapeces diagonāles ir vienādas: $AC=BD$ .
Pamata pieleņķi ir vienādi (gan abi apakšējie, gan abi augšējie): $\angle BAD=\angle CDA$ ; $\angle ABC=\angle DCB$ .
Trapeces "gala trijstūru" pamatus var izteikt ar trapeces pamatiem: $AM=DN={\frac {b-a}{2}}$ .
Līdz ar to - ja no trapeces pamata atņem viena trijstūra pamatu, atlikušā nogriežņa garumu var izteikt kā: $MD=b-{\frac {b-a}{2}}={\frac {a+b}{2}}$ .

Redzams, ka šis garums ir vienāds ar trapeces viduslīnijas garumu, tāpēc veidojas paralelograms $KLDM$ (ar visām paralelogramam piemītošajām īpašībām). Protams, tas pats ar otru pamata nogriezni $AN$ .