Bernulli sadalījums

Bernulli sadalījums

Diskrētā blīvuma funkcija 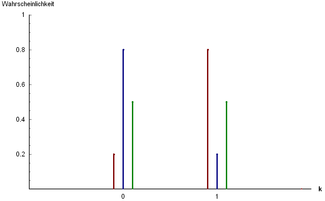Trīs Bernulli sadalījuma piemēri:   $P(x=0)=0{.}2$ un $P(x=1)=0{.}8$   $P(x=0)=0{.}8$ un $P(x=1)=0{.}2$   $P(x=0)=0{.}5$ un $P(x=1)=0{.}5$
Parametri	$0\leq p\leq 1$ $q=1-p$
Definēts	$k\in \{0,1\}$
Blīvuma funkcija	${\begin{cases}q=1-p&{\text{ja }}k=0\\p&{\text{ja }}k=1\end{cases}}$
Sadalījuma funkcija	${\begin{cases}0&{\text{ja }}k<0\\1-p&{\text{ja }}0\leq k<1\\1&{\text{ja }}k\geq 1\end{cases}}$
Vidējā vērtība	$p$
Mediāna	${\begin{cases}0&{\text{ja }}p<1/2\\\left[0,1\right]&{\text{ja }}p=1/2\\1&{\text{ja }}p>1/2\end{cases}}$
Moda	${\begin{cases}0&{\text{ja }}p<1/2\\0,1&{\text{ja }}p=1/2\\1&{\text{ja }}p>1/2\end{cases}}$
Dispersija	$p(1-p)=pq$
Vidējā absolūtā novirze	$2p(1-p)=2pq$
Asimetrijas koeficients	${\frac {q-p}{\sqrt {pq}}}$
Ekscesa koeficients	${\frac {1-6pq}{pq}}$
Entropija	$-q\ln q-p\ln p$
Momentu ģenerējošā funkcija	$q+pe^{t}$
Raksturīgā funkcija	$q+pe^{it}$
Varbūtību ģenerējošā funkcija	$q+pz$
Fišera informācija	${\frac {1}{pq}}$

Bernulli sadalījums varbūtību teorijā ir diskrēts varbūtību sadalījums, kas raksturo gadījuma lielumu, kurš pieņem divas iespējamās vērtības — 1 ar varbūtību $p$ un 0 ar varbūtību $q=1-p$. Tas ir nosaukts par godu Jākobam Bernulli.

Šis sadalījums modelē iznākumus no viena eksperimenta, kurā tiek uzdots jā/nē jautājums. To var uztvert kā biomiālā sadalījuma speciālgadījumu, kur tiek veikts viens mēģinājums ($n=1$). Otrādi skatoties, binomiālo sadalījumu var uztvert kā sadalījumu, ko iegūst saskaitot vairākus Bernulli sadalītus gadījuma lielumus.

Bernulli sadalījuma blīvuma funkcija ir

$f(k)={\begin{cases}p,&{\text{ja }}k=1,\\q=1-p,&{\text{ja }}k=0.\end{cases}}$

To var pierakstīt arī kā

$f(k)=p^{k}(1-p)^{1-k},\quad k\in \{0,1\}.$

Bernulli gadījuma lieluma $X$ matemātiskā cerība $\operatorname {E} [X]=p$, bet dispersija $\operatorname {D} [X]=pq=p(1-p)$.

Ārējās saites

• Vikikrātuvē par šo tēmu ir pieejami multivides faili. Skatīt: Bernulli sadalījums.
• Wolfram Mathworld ieraksts (angliski)