Pāriet uz saturu

Loģika

Labot saites
Vikipēdijas lapa
Loģiska izteiksme, kas uzrakstīta, izmantojot loģiskos simbolus

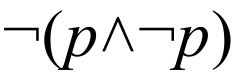
Loģika (grieķu: λογική, logiké — ‘pareizi domāt’)[1] ir zinātne par intelektuālās izziņas formām, metodēm un to savstarpējām likumsakarībām. Būtībā loģika ir zinātne par domāšanu, kura nodarbojas ar domāšanas veidu un likumu pētīšanu. Loģika ļauj pamatot savu viedokli un nenonākt pretrunās pašam ar sevi. Viens no loģikas svarīgākajiem uzdevumiem ir iemācīt apzināti izmantot loģikas likumus un domāšanas formas. Tā ļauj izprast jēdzienus un izdarīt spriedumus un secinājumus.

Loģiskie spriedumi un elementi ir atrodami visās zinātņu nozarēs.

Vārds “loģika” cēlies no sengrieķu vārda lógos, ko var tulkot dažādi – kā “prāts”, “diskurss” vai “valoda”.[2] Tradicionāli loģika tiek definēta kā domāšanas likumu vai pareizas spriešanas izpēte, un visbiežāk tā tiek saprasta saistībā ar secinājumiem vai argumentiem.[3] Spriešana ir darbība, kurā tiek izdarīti secinājumi. Argumenti ir šīs spriešanas ārējais izpausmes veids. Arguments sastāv no premisām un secinājuma.[3] Loģika interesējas par to, vai argumenti ir pareizi, proti, vai to premisas atbalsta secinājumu.[4] Šis vispārīgais raksturojums attiecas uz loģiku plašākajā nozīmē – gan uz formālo, gan neformālo loģiku, jo abas nodarbojas ar argumentu pareizības novērtēšanu.[5] Formālā loģika vēsturiski ir bijusi dominējošā joma, un daži loģiķi jēdzienu “loģika” attiecina tikai uz formālo loģiku.[6]

Formālā loģika

[labot šo sadaļu | labot pirmkodu]
Pamatraksts: Formālā loģika

Formālā loģika (jeb simboliskā loģika) pēta secināšanas struktūru, neatkarīgi no konkrētā satura. Tā izmanto formālas sistēmas, simbolus un aksiomas, lai analizētu argumentu loģisko derīgumu. Formālā loģika ietver tādus apakšvirzienus kā izteiksmju loģika (propozicionālā loģika) un predikātu loģika.

Šajā loģikas veidā svarīgi ir tikai tas, vai secinājumi loģiski izriet no premisām. Tā veido pamatu mūsdienu matemātiskajai loģikai un tiek plaši izmantota datorprogrammēšanā, algoritmu teorijā un mākslīgajā intelektā.

Neformālā loģika

[labot šo sadaļu | labot pirmkodu]
Pamatraksts: Neformālā loģika

Neformālā loģika analizē argumentus, kas izteikti dabiskajā valodā, īpašu uzmanību pievēršot argumentācijas kvalitātei, loģiskajām kļūdām (sofismiem) un retorikai. Tā nav balstīta tikai uz formāliem likumiem, bet ņem vērā arī kontekstu, nozīmi un valodas lietojumu.

Neformālā loģika ir nozīmīga filozofijā, komunikācijā, jurisprudencē un izglītībā, kur svarīgi ne vien secināt loģiski, bet arī pārliecinoši argumentēt. Tā palīdz atpazīt kļūdainus vai maldinošus argumentus un veicina kritisko domāšanu.

Loģiku pēta dažādās zinātņu nozarēs. Bieži tas notiek, pielietojot loģikas formālās metodes specifisku, ārpus tās tiešās darbības jomas esošu tēmu izpētē, piemēram, ētikā vai datorzinātnē.[7] Citkārt pati loģika kļūst par pētniecības objektu kādā citā disciplīnā. Tas var izpausties dažādos veidos — piemēram, pētot filozofiskos pieņēmumus, kas saistīti ar loģiķu izmantotajiem pamatjēdzieniem. Citas pieejas ietver loģikas interpretāciju un analīzi, izmantojot matemātiskas struktūras, kā arī formālo loģisko sistēmu abstrakto īpašību izpēti un salīdzinājumu.[8]

Matemātiskā loģika

[labot šo sadaļu | labot pirmkodu]
Pamatraksts: Matemātiskā loģika

Matemātiskā loģika ir vairāku citu zinātņu nozaru pamatā, piemēram, teorētiskas datorzinātnes un filozofiskās loģikas pamatā. Matemātiskajā loģikā pēta matemātisko pierādījumu formas, formālās valodas izteikumus un operācijas ar izteikumiem. Matemātiskā loģika apvieno vienā disciplīnā matemātiku un loģiku, aprakstot pareizai domāšanai raksturīgās formālās kārtulas.

Filozofiskā loģika

[labot šo sadaļu | labot pirmkodu]

Filozofiskā loģika ir akcentēta uz loģikas filozofiskajiem aspektiem. Tajā tiek apskatīti tādi jautājumi kā, piemēram, vai patiesība ir absolūta, vai tā tomēr ir atkarīga no prāta un uztveres. Tā ietver formālo sistēmu analīzi, kas pārsniedz klasiskās loģikas robežas, piemēram, modālo, deontisko, daudzvērtību loģiku. Filozofiskā loģika cenšas skaidrot, kā darbojas spriešana sarežģītās vai konceptuāli jutīgās situācijās, un tai ir cieša saikne ar metafiziku, semantiku un prāta filozofiju.

Loģika datorzinātnē

[labot šo sadaļu | labot pirmkodu]

Datorzinātnes loģika ir loģikas un datorzinātnes nozare, kas pēta, kā datorus var izmantot, lai automatizētu loģisko argumentāciju un precīzu, formālu spriedumu izveidi. Šajā jomā ietilpst, piemēram, automātiskie teorēmu pierādītāji, kas, izmantojot secināšanas likumus, no dotajām premisām soli pa solim izveido pierādījumu bez cilvēka iejaukšanās.[9]

Tiek izmantotas arī loģiskās programmēšanas valodas, kurās fakti tiek izteikti ar loģiskām formulām, un no tiem iespējams izdarīt secinājumus. Viens no zināmākajiem piemēriem ir Prolog, kas balstīts uz predikātu loģiku.[10]

Loģikas jēdzieni tiek pielietoti arī praktiskos datorikas uzdevumos. Klods Šenons parādīja, kā Būla algebra var tikt izmantota datoru shēmu projektēšanā. Šie principi tiek realizēti ar elektroniskajiem loģiskajiem elementiem, kuros propozīciju patiesuma vērtības tiek attēlotas ar elektriskā sprieguma līmeņiem.[11]

Radniecīgās nozares

[labot šo sadaļu | labot pirmkodu]

Loģikas vēsture

[labot šo sadaļu | labot pirmkodu]

Tiek uzskatīts, ka loģika radās pirms aptuveni trīs tūkstošiem gadu. Līdz ar to tā ir viena no senākajām zinātnēm. Lielā mērā loģika ir bijusi saistīta ar filozofiju. Līdz 19. gadsimtam loģika bija filozofijas sastāvdaļa. Tikai 20. gadsimtā tā kļuva par patstāvīgu zinātni. Loģika kļuva ne tikai par zinātni, bet arī kļuva par izziņas, darbības un komunikācijas organonu.

Starp sengrieķu filozofiem, kas lika pamatus antīkās pasaules loģikai, bija Pitagors, Zēnons Elejietis, megarieši, īpaši Eubulīds, Sokrats un Platons.[12] Liels devums Rietumu pasaules loģikas attīstībā bija arī vēlāk dzīvojošajam sengrieķu filozofam Aristotelim.

Loģikā izmantotie simboli

[labot šo sadaļu | labot pirmkodu]

Loģikā plaši tiek izmantoti dažādi simboli. Šeit ir uzskaitīti izplatītākie no tiem.

  • & vai ∧ — papildoperācijas simbols, kas attēlo saikli "un", piemēram, A&B (lasa "A un B");
  • ∨ — papildoperācijas simbols, kas attēlo loģisko disjunkciju "vai", piemēram, A∨B (lasa "A vai B");;
  • ¬ — pamatoperācijas simbols, kas attēlo noliegumu, piemēram, ¬A (lasa "ne A");
  • ~ — izmanto nolieguma attēlošanai "ne" (šī simbola vietā bieži izmanto simbolu ¬);
  • ⊕ — izmanto izslēdzošā nolieguma attēlošanai, piemēram, A⊕B (lasa "A vai B, bet ne abi");
  • → — pamatoperācijas simbols, kas norāda uz to, kas seko pēc iepriekš minētā, piemēram, A→B (lasa "ja A, tad B" vai "no A seko B");
  • ⊃ — nosacījuma simbols, līdzīga nozīme kā iepriekšējam simbolam →;
  • ≡ — simbols, kuru izmanto ekvivalences apzīmēšanai, piemēram, A≡B (lasa "A līdzvērtīgs B" vai "A ekvivalents B");
  • | — izmanto, lai apzīmēt "ne un", angliski not and;
  • ∀ — universālais kvantors, kas nozīmē "visiem ... (ir spēkā, ka)";
  • ∃ — eksistences kvantors, kas nozīmē "eksistē tāds ..., ka";
  • ∃! — eksistences kvantors, kas nozīmē "eksistē tieši viens tāds ..., ka";
  • ⊤ — loģiskais lielums, kas apzīmē tautoloģiju;
  • ⊥ — loģiskais lielums, kas apzīmē pretrunu;
  • ⊢ — norāda, ka izteikums ir pierādāms, piemēram, A⊢B nozīmē, ka "B ir pierādāms no A";
  • ⊨ — norāda uz saistību, piemēram, A⊨B nozīmē, ka "A ir semantiski saistīts ar B";
  • ∴ — simbols nozīmē "tādējādi";
  • ∵ — simbols nozīmē "tāpēc, ka".
  1. ↑ Zinātnes un tehnoloģijas vārdnīca. Rīga : Norden AB. 2001. 399. lpp. ISBN 9984-9383-5-2.
  2. ↑ «Logos | Encyclopedia.com». www.encyclopedia.com. Skatīts: 2025-05-28.
  3. 1 2 «Philosophy of logic | Definition, Problems, & Facts | Britannica». www.britannica.com (angļu). Skatīts: 2025-05-28.
  4. ↑ Hintikka Jaakko, Gabriel Sandu. What is Logic?. North Holland, 2002. 13–39. lpp.
  5. ↑ Blair, J. Anthony; Johnson, Ralph H. (2000-01-01). "Informal Logic: An Overview". Informal Logic 20 (2). doi:10.22329/il.v20i2.2262. ISSN 0824-2577.
  6. ↑ Edward Craig. Routledge Encyclopedia of Philosophy: Genealogy to Iqbal. New York : Routledge, 1996.
  7. ↑ Jaakko J. Hintikka. «Philosophy of logic | Encyclopedia Britannica». web.archive.org, 2015-04-28. 1—10. lpp. Arhivēts no oriģināla, laiks: 2015-04-28. Skatīts: 2025-05-21.
  8. ↑ J. Donald Monk. Mathematical Logic. New York, NY : Springer, 1976. 1–9. lpp. ISBN 978-1-4684-9452-5.
  9. ↑ Paulson, Lawrence C. (2018-02). "Computational logic: its origins and applications" (en). Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 474 (2210): 20170872. doi:10.1098/rspa.2017.0872. ISSN 1364-5021.
  10. ↑ O'Regan, Gerard (2016). "Introduction to the History of Computing" (en). Undergraduate Topics in Computer Science: 49. doi:10.1007/978-3-319-33138-6. ISSN 1863-7310.
  11. ↑ A dictionary of computing. Oxford ; New York : Oxford University Press. 2008. ISBN 978-0-19-923400-4.
  12. ↑ «THE HISTORY OF LOGIC» (angliski). Valdosta State University. Arhivēts no oriģināla, laiks: 2009-06-19. Skatīts: 2012-12-03.
Saturs iegūts no "https://lv.wikipedia.org/w/index.php?title=Loģika&oldid=4285824"