Slapināšana

Slapināšana ir šķidruma spēja saglabāt kontaktu ar cietu virsmu, kā rezultātā rodas bezgalīga mijiedarbība, kad abas virsmas saskaras. Slapināšanas pakāpi nosaka, vadoties pēc spēku līdzsvara starp saķeres spēku un saistvielu spēkiem. Slapināšana pēta trīs materiālu fāzes: gāzes, šķidrumus un cietvielas. Tagad slapināšana ir uzmanības centrā nanotehnoloģiju un nanozinātnes studijām daudzo nanomateriālu attīstības dēļ pēdējo 20 gadu laikā (piemēram, oglekļa šķiedra un oglekļa nanocaurulītes).
Slapināšana ir svarīga divu materiālu salipšanai vai atgrūšanai. Slapināšanas un virsmas spēki, kas kontrolē slapināšanu, atbild arī par citiem saistītiem efektiem, ieskaitot kapilāro iedarbību. Neatkarīgi no slapināšanas daudzuma, piliena forma uz cietas virsmas ir aptuveni nošķelta sfēra. Var būt dažādas slapināšanas pakāpes.
Izskaidrojums
[labot šo sadaļu | labot pirmkodu]Saistīšanās (adhezīvais) spēks starp šķidrumu un cietvielu liek šķidrumam pievilkties un izplatīties pa virsmu. Saistspēks šķidrumā liek šķidrumam atgrūsties un izveidot lodīti, lai izvairītos no kontakta ar virsmu.
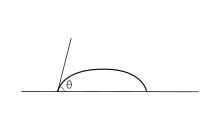
Kontakta leņķis (θ) ir leņķis, pie kura šķidruma saskaras ar cietvielu. Kontakta leņķis tiek noteikts ar rezultējošo spēku starp adhezīvo spēku un saistspēku. Kā tendence, ja pa cietas vielas virsmu izplatās piliens, kontakta leņķis samazinās. Tādējādi kontakta leņķis nodrošina apgrieztu proporcionalitāti slapināšanai.[1] Kontakta leņķis, kas mazāks par 90°(zems kontakta leņķis), parasti norāda, ka virsma slapināšanai ir labvēlīga un šķidrums izplatīsies pa lielu virsmas laukumu. Kontakta leņķis, lielāks par 90° (augsts kontakta leņķis), galvenokārt nozīmē, ka virsma slapināšanai ir nelabvēlīga, tāpēc šķidrums samazina kontaktu ar virsmu un ieņem sfēriska piliena formu. Virsmas, ko slapina ūdens, var saukt par hidrofilām virsmām, bet neslapināmas virsmas var saukt par hidrofobām virsmām.[2] Hidrofobās virsmas kontakta leņķis ir lielāks par 150°, parādot, ka gandrīz nav kontakta virsmai ar šķidrumu. Dažreiz tas tiek saukts par „Lotusa efektu”. Tabula parāda dažādus kontakta leņķus un atbilstošās cietviela/šķidrums un šķidrums/šķidrums mijiedarbības.
| Kontakta Leņķis | Slapināšanas
pakāpe |
Spēks: | |
|---|---|---|---|
| Cietvielas/Šķidruma mijiedarbība |
Šķidruma/šķidruma mijiedarbība | ||
| θ = 0 | Ideāla slapināšana | Stipra | Vāja |
| 0 < θ < 90° | Augsta slapināšana | Stipra | Stipra |
| Vāja | Vāja | ||
| 90° ≤ θ < 180° | Zema slapināšana | Vāja | Stipra |
| θ = 180° | Ideāla neslapināšana | Vāja | Stipra |

Augstas enerģijas virsmas pret zemas enerģijas virsmām
[labot šo sadaļu | labot pirmkodu]Ir divu galvenie cietvielu virsmu tipi, ar kurām šķidrumi var mijiedarboties. Tradicionāli, cietvielu virsmas ir iedalītas augstas enerģijas cietvielās un zemas enerģijas cietvielās. Cietvielas, tādas kā metāls, stikls un keramika, ir augstas enerģijas cietvielas, jo ķīmiskās saites, kas tur tos kopā (kovalentās, jonu vai metāla), ir ļoti spēcīgas un prasa daudz enerģijas to saraušanai. Lielākā daļa molekulāro šķidrumu pilnīgi slapina augstas enerģijas virsmas.
Citu veidu cietvielām ir vāji molekulu kristāli (fluorogļūdeņraži, ogļūdeņraži), kur molekulas turas kopā galvenokārt ar fizisko spēku (Van der Vālsa un ūdeņraža saites). Tā kā šīs cietvielas satur vājas saites pietiek pievadīt maz enerģijas, lai pārrautu šīs saites, tāpēc tās tiek sauktas par zemas enerģijas cietvielām. Atkarībā no izvēlētā šķidruma tipa virsmas var tikt pilnīgi vai daļēji slapinātas.[3][4]
Zemas enerģijas virsmu slapināšana
[labot šo sadaļu | labot pirmkodu]Zemas enerģijas virsmas galvenokārt mijiedarbojas ar šķidrumu, izmantojot dispersijas (Van der Vālsa) spēku. Viliama Zismana darbos ir pāris atslēgas atklājumi:
- Zismans novēroja, ka cos(θ) palielinās lineāri kā virsmas spriegums (γLV),
kad šķidruma piliens samazinās. Tādējādi viņš varēja izveidot lineāru attiecību starp cos(θ) un virsmas spraigumu (γLV), dažādiem organiskiem šķidrumiem.
- Virsma ir slapināmāka, kad γLV, θ ir mazs. Kad θ = 1, līniju krustpunktā ir kritiskais virsmas spraigums (γc) dotajai virsmai. Kritiskais
virsmas spriegums ir svarīgs parametrs, jo tas raksturīgs tikai cietvielām.
- Zinot cietvielas virsmas kritisko spriegumu, ir iespējams paredzēt kā tiks slapināta virsma.
- Virsmas slapināšanas pakāpi nosaka pēc visattālākajām ķīmiskajām grupām cietvielā.
- Atšķirības slapināšanas pakāpē starp virsmām, kas ir līdzīgas pēc struktūras ir saistīts
ar atšķirībām atomu izvietojumā. Piemēram, ja virsmā ir sazarotas ķēdes, tās ir vājākas nekā virsmas ar taisnā ķēdē izvietotiem atomiem.
Ideālas cietas virsmas
[labot šo sadaļu | labot pirmkodu]Ideāla cieta virsma ir tā, kas ir perfekti līdzena, stingra, plakana ķīmiski homogēna un kontakta leņķis ir nulle. Nulles histerēze (definīcija: Fizikālās sistēmas reakcija pret ārējo iedarbību atkarībā no tā, vai šī mijiedarbība parādās pirmo reizi vai ir bijusi arī agrāk.) nozīmē, ka piliena leņķi abās pusēs ir vienādi. Turklāt uz ideālas virsmas piliens atgriezīsies oriģinālajā formā, pēc fiziskās iedarbības noņemšanas.[2][5] Turpmākie vienādojumi būs precīzi tikai ideālām virsmām un ir derīgi, ja virsmas un piliens nekustas un fāzes robežlīnijā pastāv līdzsvars.
Enerģijas samazināšanas, trīs fāzēs
[labot šo sadaļu | labot pirmkodu]
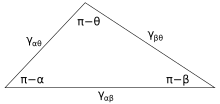
Līdzsvarā summārais spēks darbojas gar robežlīniju un starp šiem trīs posmiem spēkam jābūt nullei. Summārā spēka virziens gar katru saskarnes komponenti ir dots:
kur α, β, un θ ir parādītie leņķi un γij ir virsmas enerģija starp divām fāzēm. Šī attiecība var tikt izteikta analoģiski Neimana trīsstūrim. Neimana trīsstūris saskaņā ar ģeometriskiem ierobežojumiem, piemērojot sinusa un kosinusa likumu, izveido attiecību, kas raksturo starpfāžu leņķu atkarību no virsmas enerģijas radītājiem.[6]
Šo trīs virsmu enerģijas veido trīsstūra malas, to ierobežo trijstūra nevienlīdzība, γij < γjk + γik, kas nozīmē, ka neviens no virsmas spriegumiem nevar pārsniegt abu pārējo summu.
Vienkāršošana uz plaknes ģeometriju, Junga attiecība
[labot šo sadaļu | labot pirmkodu]Ja β fāze ir aizvietota ar stingru cietu virsmu, tad β = π, un otrs summārais spēks novienkāršojas līdz Junga vienādojumam.

kas parāda virsmas spraigumu starp trijām fāzēm: cietvielu, šķidrumu un gāzi. Pēc tam var prognozēt kontaktu leņķi starp pilienu uz cietas virsmas no zināšanām par iesaistītajām trim virsmas enerģijām. Šis vienādojums ir pielietojams arī tad, ja gāzes fāze ir cits šķidrums, kas nesajaucas ar otru pilienu šķidrajā fāzē.
Gludas virsmas un Junga kontakta leņķis
[labot šo sadaļu | labot pirmkodu]Junga vienādojums der, kad piliens balstās uz pilnīgi līdzenu un cietu virsmu. Daudzos gadījumos virmas ir tālu no šīs ideālās situācijas, un divas ir aprakstītas šeit: gadījums ar raupju, nelīdzenu virsmu un gadījums ar gludu virsmu, kas tomēr ir reālas (gandrīz gludas). Pat uz perfekti līdzenas virsmas piliens pieņem dažādus kontakta leņķus, sākot ar tā sauktiem pietuvināšanās kontakta leņķiem, , līdz tā sauktajiem attālināšanās kontakta leņķiem, . Līdzsvara kontakta leņķis () var tikt aprēķināts no un kā Tadmors ir konstatējis,[8]
kur
Junga-Duprē vienādojums un izplatīšanās koeficients
[labot šo sadaļu | labot pirmkodu]Junga-Duprē vienādojums (Tomass Jungs 1805, Levis Duprē 1855) diktē, ka γSG un γSL nevar būt lielāki par abu pārējo virsmu enerģiju summu. No šī ierobežojuma izriet, ka var prognozēt pilnīgu slapināšanu, kad γSG > γSL + γLG un nulles slapināšana, kad γSL > γSG + γLG. Junga-Duprē vienādojuma problēma ir, ka nav līdzsvara gadījuma starp 0 un 180°
Noderīgs parametrs, lai novērtētu slapināšanu ir izplatīšanās parametrs S,
Kad S > 0, šķidrums pilnīgi slapina virsmu (pilnīga slapināšana). Kad S < 0, tad ir nepilnīga slapināšana.
Savienojot izplatīšanās parametra definīciju ar Junga attiecību, izveidojas Junga-Duprē vienādojums
Kam fizikāli risinājumi θ. Kad S<0
Neideālas rupjas virsmas
[labot šo sadaļu | labot pirmkodu]
Atšķirībā no ideālām virsmā, reālā virsma nav perfekti līdzena, stingra, un ķīmisko viendabīga. Šādas novirzes no idealitātes noved pie parādības, kuru sauc par histerēzi. Kontaktu leņķu histerēzi ir definēta kā starpība starp pietuvināšanās leņķi (θa) un attālināšanās (θr) kontakta leņķi.[9]
Kontaktu leņķu histerēze ir būtiska kontakta līnijas nobīde, pēc kā seko piliena pievilkšanās vai atgrūšanās. Pietuvināšanās leņķis ir maksimālais stabilais leņķis, kur attālināšanās kontakta leņķis ir minimālais stabilais leņķis. Kontaktu leņķu histerēze parādās, jo ir vairāki termodinamiski stabili kontakta leņķi uz reālas cietvielas. Šie mainīgie termodinamiski stabilie stāvokļu leņķi ir zināmi kā metastabilie stāvokļi.[5]
Piemēram, kustības fāzes robežās, iesaistot pietuvināto un attālināto kontaktu leņķi, ir pazīstama kā dinamiskā slapināšana. Kad kontakta līnija pietuvinās, pārklājot lielāku virsmu ar šķidrumu, kontakta leņķis tiek palielināts un galvenokārt ir saistīts ar kontakta līnijas ātrumu. Ja kontakta līnijas ātrums tiek palielināts bez ierobežojumiem, kontakta leņķis palielinās, un, kad tas sasniedz 180° gāzes fāze atradīsies plānā kārtā starp šķidrumu un cietvielu. Kinētiskajai enerģijai nav līdzsvara, kā rezultātā kontaktlīnija pārvietojas ar tik lielu ātrumu, un slapināšana nav iespējama. Rupjas virsmas tekstūras var iedalīt divās kategorijās: Homogēnās un heterogēnās. Homogēns slapināšanas režīms ir tad, kad šķidrums aizpilda nelīdzenās virsmas krokas. Heterogēns režīms ir, kur virsmas ir kā saliktas no divu tipu gabaliem. Tādām virsmām ir dažāda veida ietekme uz šķidrumu slapināšanas kontakta leņķiem. Keisija-Bakstera un Venzela modeļi ir divi galvenie , kas mēģina aprakstīt nelīdzenas, saliktas virsmas slapināšanu. Kaut gan šos vienādojumus var pielietot vienīgi tad, kad piliena izmērs ir ievērojami lielāks salīdzinot ar virsmas negludumiem.[10]
Venzela modelis
[labot šo sadaļu | labot pirmkodu]
Venzela modelis (Robert N. Wenzel 1936) apraksta homogēnus slapināšanas režīmus un ir definēts nākamajā vienādojumā par kontakta leņķi uz nelīdzenas virsmas.[10]
kur ir šķietamais kontakta leņķis, kurš atbilst stabilajam līdzsvara stāvoklim. Nelīdzenuma koeficients r, ir lielums, kā virsmas nelīdzenums ietekmē homogēnu virsmu. Nelīdzenuma koeficients ir definēts kā patiesā laukuma attiecība pret šķietamo laukumu.
θ ir Junga kontakta leņķis kā definēts pie ideālām virsmām. Venzela modelis demonstrē arī, ka kontakts leņķis raupjai virsmai atšķiras no raksturīgajiem kontaktu leņķiem, taču tas neapraksta kontaktu leņķu histerēzi.[11]
Keisija-Bakstera modelis
[labot šo sadaļu | labot pirmkodu]
Kad jātiek galā ar heterogēnām virsmām, Venzela modelis nav pilnīgs. Sarežģītāks modelis ir vajadzīgs, lai izmērītu kā šķietamais kontakta leņķis mainās, kad dažādi materiāli ir iesaistīti. Kas ir heterogēna virsma ir izskaidrota izmantojot Keisija-Bakstera vienādojumu (Keisija likums):[10]
kur rf ir slapjās virsmas laukuma nelīdzenuma koeficients un f ir cietvielas daļa, kas tiek slapināta ar šķidrumu. Svarīgi ir saprast, kad f=1 un rf=r, Keisija-Bakstera vienādojums, kļūst par Venzela vienādojumu. Ja ir daudz dažādu virsmas nelīdzenuma frakciju, katra frakcija no kopējās virsmas tiek apzīmēta ar . Visu fi summa ir vienāda ar 1 no kopējās virsmas. Keisija-Bakstera vienādojumu var pārveidot šādā vienādojumā:[12]
Šeit γ ir Keisija-Bakstera virsmas spraigums starp šķidrumu un tvaiku, γi,sv ir cietvielas un tvaika virsmas spraigums katrai komponentei un γi,sl ir cietvielu šķidruma virsmas spriegums katrai komponentei. Gadījums, ko ir vērts pieminēt, ir, kad šķidruma piliens ir novietots uz paliktņa un izveido mazas gaisa kabatiņas zem tā. Šīs divu komponentu sistēmas gadījums ir parādīts:[12]
Šeit galvenā atšķirība, ko vajadzētu ievērot, ir, ka šeit nav virsmas spraigums starp šķidrumu un tvaiku otrajai virsmas spraiguma komponentei. Šis ir pieņēmuma dēļ, ka gaisa virsma, kas ir pakļauta, atrodas zem piliena un ir vienīgi cits substrāts sistēmā. Pēc tam vienādojums ir izteikts kā (1-f). Tāpēc Keisija vienādojums var vienkārši tikt atvasināts no Keisija-Bakstera vienādojuma. Eksperimentālie rezultāti attiecībā uz Venzela virsmas īpašībām salīdzinot ar Keisija-Bakstera sistēmu uzrādīja ietekmi uz Junga kontakta leņķi no 180 ° līdz 90 °, šo reģionu klasificē ar Keisija-Bakstera modeli. Šķidruma-gaisa kompozītu sistēma lielā mērā ir hidrofoba. Pēc šī punkta notiek asa pāreja uz Venzela režīmu, kas tika atrasts, kur piliens slapina virsmu, bet ne nelīdzenumu bedrītes.
Prekursora plēve
[labot šo sadaļu | labot pirmkodu]Ar augstas izšķirtspēju attēlu parādīšanos, zinātnieki sāka iegūt eksperimentālos datus, kuri viņus noveda pie jautājuma par Keisija-Bakstera vienādojumu, kad tiek aprēķināts šķietamais kontakta leņķis. Šī grupiņa zinātnieku pieņēma, ka šķietamais kontakta leņķis ir lielā mērā atkarīgs no trīskāršās līnijas, kura ir kontaktā ar heterogēno (nelīdzeno) virsmu, kura nevar balstīties uz nelīdzeno virsmu kā rakstīts teorijā. Teorijā pilienam būtu jāseko virsmas nelīdzenumam. Šīs trīskāršās līnijas locīšanās ir nelabvēlīga un nav novērojama reālās dzīves situācijās. Teorija, kas saglabā Keisija-Bakstera vienādojumu, kamēr tajā pašā laikā izskaidro trīskāršās līnijas locīšanās minimizētās enerģijas klātbūtnes stāvokli ar prekursora plēves ideju. Šī submikrometra biezuma plēvīte izvirza priekšā piliena kustību trīskāršās līnijas tuvumā. Turklāt šī prekursora plēve atļauj trīskāršajai līnijai locīties un ieņemt dažādas formas, kas sākotnēji tika uzskatīts, ka tas nav vēlams. Prekursora šķidrums ir novērots izmantojot vides skenēšanas elektronu mikroskopu (ESEM) virsmās, kurās ir poras. Ar prekursora plēves koncepta ievadu, trīskāršā līnija var sekot enerģētiski mainīgai uzbūvei un tomēr pareizi izskaidrot Keisija-Bakstera modeli.[13]
„Ziedlapas efekts pret „Lotosa efektu’’[14]
[labot šo sadaļu | labot pirmkodu]
Raksturīgā virsmas hidrofobija var tikt uzlabota sadalot virsmas tekstūru dažādos garumos un nelīdzenuma mērogos. Sarkanā roze izmanto šo priekšrocību izmantojot mikro un nanomikrostruktūras hierarhiju uz katras ziedlapas nodrošinot pietiekošu raupjumu superhidrofobijai. Precīzāk katrai rozes ziedlapai ir vesels kopums mikrokārpiņu uz virsmas un katra kārpiņai savukārt ir daudz nanokrokas. Termins „Ziedlapas efekts” apraksta faktu, ka ūdens piliens uz rozes ziedlapas virsmas ieņem sfērisku formu un nevar novelties no ziedlapas pat, ja tā ir „kājām gaisā”. Ūdens piliens saglabā sfērisko formu, ziedlapas superhidrofobitātes dēļ (kontakta leņķis apmēram 152.4°), bet nenovelsies, jo ziedlapas virsmai ir liels saistīšanās spēks ar ūdeni.
Kad salīdzina „ziedlapas efektu” ar „lotosa efektu” ir svarīgi atzīmēt pāris pārsteidzošas atšķirības. Virsmas struktūra lotosa ziedlapai un rozes ziedlapai var tikt izmantots, lai izskaidrotu divus dažādus efektus. Lotosa ziedlapai ir viendabīgi raupja virsma un maza kontaktu leņķu histerēze, kura nozīmē, ka ūdens piliens nevar slapināt mikrostruktūras krokas. Tas ļauj gaisam palikt krokās, izraisot heterogēnu virsmu no šāda sastāva: gaisa un cietvielas. Kā rezultātā saistīšanās spēks starp ūdens un cietvielas virsmu ir ļoti mazs, ļaujot ūdenim novelties viegli (tā ir „pašattīrīšanās parādība”).
No otras puses rozes ziedlapas mikro- un nanostruktūra ir lielāka mērogā kā lotosa lapas, kas ļauj šķidruma plēvei piepildīt struktūru. Lai gan šķidrums var iekļūtu lielāka mēroga krokās, bet tas nevar iekļūt mazākās krokās. Šis ir zināms kā Keisija piesātinātās slapināšanas režīms. Kad šķidrums var slapināt lielāka mēroga krokas, saistīšanās spēks starp ūdeni un cietvielu ir ārkārtīgi liels. Tas izskaidro kāpēc ūdens piliens nenokritīs pat, ja ziedlapa ir sasvērta jebkādā leņķī vai apgriezta otrādi. Kaut gan šis efekts izgāžas pie nosacījuma, ja ūdens piliena tilpums ir lielāks par 10 µl, jo balanss starp svaru un virsmas spraigumu ir pārsniegts.
Pāreja no Keisija-Bakstera uz Venzela modeli
[labot šo sadaļu | labot pirmkodu]
Keisija-Bakstera modelī, piliens sēž saliktās virsmas augšā ar gaisu iesprostotu zem tā. Slapināšanas pārejas laikā no Keisija stāvokļa uz Venzela stāvokli, gaisa kabatas vairs nav termodinamiski stabilas un šķidrums sāk veidot kodolu no piliena vidus izveidojot "sēnes stāvokli".[15] Iespiešanās nosacījums ir dots vienādojumā:
kur
- θC ir kritiskais kontakta leņķis
- Φ ir cietvielas/šķidruma daļas, kur piliens kontaktējas ar virsmu
- r ir cietvielas raupjums (nelīdzenums) (Līdzenām virsmām, r = 1)

Iespiešanās krokās izplatās ārpus piliena, lai mazinātu virsmas enerģiju līdz tā sasniedz piliena malas, tādējādi nonākot pie Venzela stāvokļa. Kontakta leņķis, pie kura izplatīšanās parādās atrodas starp 0 ≤ θ < π/2.[16]
Venzela modelis ir derīgs starp θC < θ < π/2. Ja kontakta leņķis ir mazāks kā θC, iespiešanās krokās izplatās ārpus piliena un šķidruma plēve izveidojās pa virsmu. Plēve izlīdzina virsmas nelīdzenumu un Venzela modelis vairs nav spēkā. Šajā stāvoklī, līdzsvara stāvoklis un Junga attiecība pagarinās:
Ar optimālu virsmas raupjumu ir iespējams iegūt pārvietojumu starp abiem superhidrofobiem reģioniem. Galvenokārt, jo raupjāka virsma, jo hidrofobāka tā ir.
Izplatīšanās dinamika
[labot šo sadaļu | labot pirmkodu]Ja piliens ir novietots uz gludas, horizontālas virsmas, tas visbiežāk nav līdzsvara stāvoklī. Tātad tas izplūst līdz iegūst līdzsvara stāvokli un kontakta rādiuss ir sasniegts (daļēja slapināšana). Vienlaikus ņemot vēra kapilaritāti (uzsūkšanos), gravitāciju un viskozitāti, piliena rādiuss var tikt izteikts kā laika funkcija.[17]
Pilnīgai slapināšanas situācijai, piliena rādiuss jebkurā izplatīšanās brīdī ir iegūstams pēc šādas funkcijas:
kur
- γLG = Virsmas spraigums šķidrumam
- V = Piliena tilpums
- η = Šķidruma viskozitāte
- ρ = Šķidruma blīvums
- g = Gravitācijas konstante
- λ = Formas faktors λ = 37.1 m−1
- t0 = Eksperimentālais aizkavēšanās laiks
- re = Piliena rādiuss vienādojumā.
Virsmaktīvo vielu slapināšanas efekts
[labot šo sadaļu | labot pirmkodu]Daudzos tehnoloģiskajos procesos vajadzīga kontrolēta šķidruma izplatīšanās pa cietu virsmu. Kad piliens ir novietots uz virsmas, tas var slapināt pilnīgi, daļēji vai neslapināt virsmu. Samazinot virsmas spriegumu ar virsmaktīvajām vielām, neslapinošais materiāls var tikt izgatavots, lai kļūtu par daļēji slapinošu vai pilnīgi slapinošu materiālu. Piliena liekā brīvā enerģija (σ) uz ciets virsmas ir:[18]
- γ ir šķidruma-tvaika starpfāžu spriegums
- γSL ir cietvielas-šķidruma starpfāžu spriegums
- γSV ir cietvielas-tvaika starpfāžu spriegums
- S ir šķidruma-tvaika saskares laukums
- P ir pārsniegtais spiediens šķidrumā
- R Piliena pamata rādiuss
Balstīts uz šo vienādojumu, pārsniegtās brīvās enerģijas minimizēšana, kad γ samazinās, γSL samazinās, vai γSV palielinās. Virsmaktīvās vielas ir absorbētas uz šķidruma-tvaika, cietvielas-šķidruma un cietvielas-tvaika saskares, kas pārveido hidrofobo materiālu slapināšanas īpašības, lai samazinātu brīvo enerģiju. Kad virsmaktīvās vielas ir absorbētas uz hidrofobas virsmas, galvenās polārās grupas saskaras šķidrumā, ar asti norādot uz ārpusi. Citās hidrofobās virsmās, virsmaktīvās vielas var veidot divus slāņus uz cietvielas, izraisot, ka tā kļūst vēl hidrofobāka. Dinamiskais piliena rādiuss var būt raksturots kā piliens, kas sāk izplatīties. Tādā veidā kontakta leņķis mainās pamatā pēc šī vienādojuma:[18]
- θ0 ir sākuma kontakta leņķis
- θ∞ ir beigu kontakta leņķis
- τ ir virsmaktīvās vielas pāreja laika grafikā
Kad virsmaktīvā viela ir absorbēta, cietvielas-tvaika virsmas spraigums palielinās un piliena malas kļūst hidrofilas. Kā rezultātā, piliens izplūst pa virsmu.
Skatīt arī
[labot šo sadaļu | labot pirmkodu]Atsauces
[labot šo sadaļu | labot pirmkodu]- ↑ Sharfrin, E.; Zisman, William A. (1960). "Constitutive relations in the wetting of low energy surfaces and the theory of the retraction method of preparing monolayers". The Journal of Physical Chemistry 64 (5): 519–524. doi:10.1021/j100834a002.
- ↑ 2,0 2,1 N. Eustathopoulos; Nicholas, M.G. and Drevet B. Wettability at high temperatures. Oxford, UK : Pergamon, 1999. ISBN 0-08-042146-6.
- ↑ M.E Schrader, Loeb, G.I. Modern Approaches to Wettability. Theory and Applications. New York : Plenum Press, 1992. ISBN 0-306-43985-9.
- ↑ de Gennes, P.G. (1985). "Wetting: statics and dynamics". Reviews of Modern Physics 57 (3): 827–863. Bibcode 1985RvMP...57..827D. doi:10.1103/RevModPhys.57.827.
- ↑ 5,0 5,1 Johnson, Rulon E. (1993) in Wettability Ed. Berg, John. C. New York, NY: Marcel Dekker, Inc. ISBN 0-8247-9046-4
- ↑ J.S. Rowlinson, Widom, B. Molecular Theory of Capillarity. Oxford, UK : Clarendon Press, 1982. ISBN 0-19-855642-X.
- ↑ T. S. Chow (1998). "Wetting of rough surfaces". Journal of Physics: Condensed Matter 10 (27): L445. Bibcode 1998JPCM...10L.445C. doi:10.1088/0953-8984/10/27/001.
- ↑ Tadmor, Rafael (2004). "Line energy and the relation between advancing, receding and Young contact angles". Langmuir 20 (18): 7659–64. doi:10.1021/la049410h. PMID 15323516.
- ↑ Robert J. Good (1992). "Contact angle, wetting, and adhesion: a critical review". J. Adhesion Sci. Technol. 6 (12): 1269–1302. doi:10.1163/156856192X00629.
- ↑ 10,0 10,1 10,2 Abraham Marmur (2003). "Wetting of Hydrophobic Rough Surfaces: To be heterogeneous or not to be". Langmuir 19 (20): 8343–8348. doi:10.1021/la0344682.
- ↑ Marmur, Abraham (1992) in Modern Approach to Wettability: Theory and Applications Schrader, Malcolm E. and Loeb, Geroge New York: Plenum Press
- ↑ 12,0 12,1 Whyman, G.; Bormashenko, Edward; Stein, Tamir (2008). "The rigirious derivation of Young, Cassie–Baxter and Wenzel equations and the analysis of the contact angle hysteresis phenomenon". Chemical Physics Letters 450 (4–6): 355–359. Bibcode 2008CPL...450..355W. doi:10.1016/j.cplett.2007.11.033.
- ↑ Bormashenko, E. (2008). "Why does the Cassie–Baxter equation apply?". Colloids and Surface A: Physicochemical and Engineering Aspects 324: 47–50. doi:10.1016/j.colsurfa.2008.13.025.
- ↑ Lin, F.; Zhang, Y; Xi, J; Zhu, Y; Wang, N; Xia, F; Jiang, L (2008). "Petal Effect: Two major examples of the Cassie–Baxter model are the "Petal Effect" and Lotus Effect". A superhydrophobic state with high adhesive force". Langmuir 24 (8): 4114–4119. doi:10.1021/la703821h. PMID 18312016.
- ↑ Okumura, K.; Okumura, K (2008). "Wetting transitions on textured hydrophilic surfaces". European Physical Journal 25 (4): 415–424. Bibcode 2008EPJE...25..415I. doi:10.1140/epje/i2007-10308-y. PMID 18431542.
- ↑ Quere, D.; Thiele, Uwe; Quéré, David (2008). "Wetting of Textured Surfaces". Colloids and Surfaces 206 (1–3): 41–46. doi:10.1016/S0927-7757(02)00061-4.
- ↑ Härth M., Schubert D.W., Simple Approach for Spreading Dynamics of Polymeric Fluids, Macromol. Chem. Phys., 213, 654–665, 2012, DOI: 10.1002/macp.201100631
- ↑ 18,0 18,1 K.S. Lee; Ivanova, N; Starov, VM; Hilal, N; Dutschk, V (2008). "Kinetics of wetting and spreading by aqueous surfactant solutions". Advances in colloid and interface science 144 (1–2): 54–65. doi:10.1016/j.cis.2008.08.005. PMID 18834966.





















![{\displaystyle r(t)=r_{e}\left[1-\exp \left(-\left({\frac {2\gamma _{LG}}{r_{e}^{12}}}+{\frac {\rho g}{9r_{e}^{10}}}\right){\frac {24\lambda V^{4}(t+t_{0})}{\pi ^{2}\eta }}\right)\right]^{\frac {1}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3b0783644473ffde23684e6406bf84b8f9865ea)
![{\displaystyle r(t)=\left[\left(\gamma _{LG}{\frac {96\lambda V^{4}}{\pi ^{2}\eta }}\left(t+t_{0}\right)\right)^{\tfrac {1}{2}}+\left({\frac {\lambda (t+t_{0})}{\eta }}\right)^{\tfrac {2}{3}}{\frac {24\rho gV^{\frac {3}{8}}}{7\cdot 96^{\frac {1}{3}}\pi ^{\frac {4}{3}}\gamma _{LG}^{\frac {1}{3}}}}\right]^{\frac {1}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f481593e45a4dc9d2b93f7fb5d267ddc764da88)

