Tēlotāja ģeometrija

Krāsainais telpiskais attēls ir lokomotīves aksonometrija, melnabaltie plakanie attēli ir šīs lokomotīves kompleksais rasējums, tajā izmantoti pieci (no sešiem) pamatskati: virsskats, kreisais un labais sānskats, mugurskats, pretskats

Tēlotāja ģeometrija ir ģeometrijas sadaļa, kurā telpiski objekti tiek attēloti kā plakani. Tā tiek izmantota inženierijā, arhitektūrā, arī dizainā un mākslā.

Projicēšana

Projicēšanas veidi

Kuba paralēlā projicēšana: tainsleņķa (pa labi), slīpleņķa (pa kreisi)

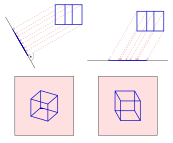
Telpiskus objektus attēlo, izmantojot vairākas metodes. Inženiergrafikā attēlošanas metožu pamatā ir projekcijas. Izšķir divus projicēšanas veidus: centrālajā projicēšanā punkta projekciju iegūst, velkot projicējošo staru no projekcijas centra caur projicējamo punktu uz projekciju plakni; paralēlajā projicēšanā projekcijas centrs atrodas bezgalīgi tālu un projicējošie stari ir savstarpēji paralēli, punkta projekciju iegūst, velkot projicējošo staru caur projicējamo punktu uz projekciju plakni. Savukārt, paralēlās projekcijas iedala vēl divos veidos: taisnleņķa jeb ortogonālās, ja projicējošie stari ir perpendikulāri projekciju plaknei; slīpleņķa jeb klinogonālās, ja projicējošie stari nav perpendikulāri projekciju plaknei. Tādējādi projicēšanā izšķir šādus elementus: telpisku objektu, projekciju plakni $\Pi$, projekcijas centru $S$ (centrālās projicēšanas gadījumā), projicēšanas virzienu $v$ (paralēlajā projicēšanā, sakrīt ar projicējošo staru virzienu).

Kuba centrālā projicēšana

Attēlojuma veidi

Rasējumam, telpiska objekta tehniskās dokumentācijas grafiskajam dokumentam, būtu jābūt uzskatāmam un viegli izmērojamam, taču neviens no projicēšanas veidiem nenodrošina abus nosacījumus vienlīdz kvalitatīvi. Centrālo projicēšanas metodi izmanto arhitektūrā perspektīvas konstruēšanai, šiem attēliem piemīt laba uzskatāmība, taču tie ir grūti konstruējami un mērāmi. Paralēlās projekcijas ir vieglāk konstruēt un mērīt, taču šādi iegūti attēli ir slikti uzskatāmi, jo ļoti atšķiras no īstenībā redzamā. Viena projekcija pilnībā neraksturo telpiskus objektus, tāpēc projekcijas jāveido vairākās plaknēs vai jāpievieno papildu informācija.

Apzīmējums Eiropas jeb pirmā oktanta (ISO) un Amerikas jeb trešā oktanta (US) koordinātu sistēmai

Kompleksais rasējums

Kompleksais rasējums sastāv no objekta projekcijām trīs vai vairāk projekciju plaknēs. Komplekso rasējumu veic trīsplakņu kaktā, kurš sastāv no trim savstarpēji perpendikulārām plaknēm, kuras sadala telpu astoņās daļās (kaktos), kuras sauc par oktantiem. Pēc ISO, objekts tiek attēlots pirmajā oktantā (Eiropas sistēma). (Ziemeļamerikā objektus pieņemts attēlot trešajā oktantā. Apvienotajā Karalistē sastopamas abas sistēmas.) Horizontālo projekciju plakni pieņemts apzīmēt ar $\Pi _{1}$, frontālo — ar $\Pi _{2}$, profilo — ar $\Pi _{3}$. Šīs trīs plaknes šķeļas pa savstarpēji perpendikulārām taisnēm $x$, $y$, $z$, kuras krustojas punktā $O$. Šīs taisnes sauc par projekciju jeb koordinātu asīm, punktu $O$ — par koordinātu sistēmas sākumpunktu.

Kādu punktu ievieto trīsplakņu kakta pirmajā (I) oktānā un ortogonāli projicē uz katru no trim plaknēm. Projicējošā stara un projekciju plaknes krustpunktā atrodas punkta projekcija ar tādu pašu nosaukumu (lielo burtu vai ciparu) kā projicējamajam punktam, bet ar indeksu, kurš ir tāds pats kā atbilstošās projekciju plaknes indekss (1, 2, 3). Plaknē $\Pi _{1}$ atrodas punkta horizontālā projekcija jeb virsskats, $\Pi _{2}$ atrodas frontālā projekcija jeb pretskats, $\Pi _{3}$ — profilā projekcija jeb kreisais sānskats. Punkta stāvokli telpā nosaka trīs koordinātas ($x$, $y$, $z$).

Trīsplakņu kakta modeli ar visām projekcijām izklājot vienā plaknē, iegūst plakanu rasējumu. Taisnes, kuras savieno punkta projekcijas, sauc par kārtotājām taisnēm (kompleksajā rasējumā tās vienmēr ir perpendikulāras projekciju asīm). Komplekso rasējumu var attēlot, nerādot projekciju asis, to sauc par bezasu rasējumu.

Aksonometrija

Aksonometrijā objekts tiek attēlots vienā projekciju plaknē. Šis attēlojuma veids atšķiras no kompleksā rasējuma ar labu uzskatāmību. Taču aksonometriskais attēls ir grūtāk konstruējams, tas attēlo objektu tikai vienā rakursā. Aksonometrijā visi mērījumi jāveic tikai triju koordinātu asu virzienos.

Kāds punkts, kas atrodas koordinātu sistēmā, tiek projicēts uz projekciju plaknes kopā ar koordinātu sistēmu, iegūstot punkta projekciju (primārā projekcija) un koordinātu sistēmas projekciju (aksonometrisko koordinātu sistēmu). Aksonometrijā nepieciešama arī punkta horizontālās projekcijas projekcija projekciju plaknē (sekundārā projekcija).

Sagrozījuma koeficienti ir aksonometrisko koordinātu sistēmas attiecības pret īstajām koordinātām.

$k_{x}={\frac {x'}{x}}$, $k_{y}={\frac {y'}{y}}$, $k_{z}={\frac {z'}{z}}$,

kur $k_{x}$, $k_{y}$, $k_{z}$ ir sagrozījuma koeficienti attiecīgi x ass, y ass, z ass virzienā; $x$, $y$, $z$ ir attālums no koordinātu sākumpunkta līdz koordinātai uz attiecīgi x, y, z ass īstajā koordinātu sistēmā; $x'$, $y'$, $z'$ ir attālums no koordinātu sākumpunkta līdz koordinātai uz attiecīgi x, y, z ass aksonometriskajā koordinātu sistēmā. Ja visi trīs sagrozījuma koefiecienti ir vienādi, pastāv izometrija. Ja divu asu sagrozījuma koeficienti ir vienādi, pastāv dimetrija. Ja visi trīs sagrozījuma koeficienti ir atšķirīgi, pastāv trimetrija.

Aksonometrijas pamatteorēma (Polkes teorēma) nosaka, ka aksonometrisko asu virzienus un sagrozījuma koeficientus var izvēlēties brīvi. Taču praksē nepieciešams veidot uzskatāmu attēlu, pareizi izvēloties attēla plaknes novietojumu un projicējošo staru leņķi pret to. Parasti izmanto kādu no standarta aksonometrijas veidiem: ortogonālo izometriju, ortogonālo dimetriju, frontālo izometriju, frontālo dimetriju, horizontālo izometriju (pirmie divi veidi ir ortogonālā jeb taisnleņķa aksonometrija, pēdējie trīs — klinogonālā jeb slīpleņķa). Aksonometrijas veidu izvēlas, ņemot vērā attēla uzskatāmību un konstruēšanas parocību.

Ortogonālajā izometrijā īstās koordinātu asis un objekts novietots slīpi pret projekciju plakni, savukārt, projicēšanas virziens ir perpendikulārs šai plaknei. Visas trīs koordinātu plaknes veido ar projekciju plakni 120° leņķi, sagrozījuma koeficienti visu trīs asu virzienos ir 0,82. Praksē izmanto reducēto sagrozījuma koeficientu, kura vērtība ir 1, rezultātā attēls ir 1,22 reizes lielāks. Šajā izometrijā riņķa līnijas attēlojas par elipsēm, tomēr praksē tās aizstāj ar ovāliem — cirkuļlīknēm ar četriem centriem un diviem rādiusiem.

Attēlu transformācijas

Lai noteiktu uzrasētā objekta sastāvdaļu ģeometriskos parametrus (garumus, laukumus, leņķus), šiem elementiem jāatrodas speciālās stāvotnēs pret projekciju plaknēm. Visbiežāk lieto divas projekciju transformāciju (pārveidojumu) metodes: projekciju plakņu maiņu un pagriešanu.

Izmantojot projekciju plakņu maiņas metodi, netiek mainīta objekta stāvotne telpā, tiek mainīta viena no esošajām projekciju plaknēm, tās vietā ieviešot jaunu projekciju plakni, kas ir perpendikulāra saglabātajai projekciju plaknei un ir vēlamā stāvotnē pret objektu.

Izmantojot pagriešanas metodi, prokeciju planes netiek mainītas, objekts tiek pagriezts vēlamā stāvotnē pret kādu no projekciju plaknēm. Pagriešanai izmanto rotācijas asis, kuras ir perpendikulāras kādai no projekciju plaknēm, vai rotācijas asis, kuras ir paralēlas kādai no projekciju plaknēm.

Ģeometriskie objekti un to projicēšana

Taisnes

Taisni telpā nosaka divi tās punkti. Taines ar horizontālo projekciju plakni $\Pi _{1}$ veido leņķi $\alpha$, ar frontālo $\Pi _{2}$ — leņķi $\beta$, ar profilo $\Pi _{3}$ — leņķi $\gamma$. Atkarībā no stāvokļa pret projekciju plaknēm taisnes iedala vispārīgas stāvotnes (nav ne paralēlas, ne perpendikulāras nevienai projekciju plaknei), līmeņa (paralēla projekciju plaknei), projicējošās taisnēs (perpendikulāra projekciju plaknei). Līmeņa un projicējošās taisnes vienā jēdzienā sauc par speciālās stāvotnes taisnēm. Horizontālajai projekciju plaknei paralēlu taisni sauc par horizontāli, frontālajai paralēlu — par frontāli, profilajai paralēlu — par profilu taisni. Horizontālajai projekciju plaknei parpendikulāru taisni sauc par horizontāli projicējošu taisni, frontālajai perpendikulāru — par frontāli projicējošu, profilajai perpendikulāru — par profili projicējošu.

Divas taisnes var būt savstarpēji paralēlas (atrodas vienā plaknē un nekrustojas), krustiskas (atrodas vienā plaknē un tām ir viens kopīgs punkts) vai šķērsas (nav paralēlas un tām nav kopīgu punktu).

Leņķa malas ir krustiskas taisnes. Ja leņķa malas ir paralēlas projekciju plaknei, leņķis projicējas patiesajā lielumā. Ja leņķa malas nav paralēlas projekciju plaknei, leņķis attēlojas sagrozīti. Taisns leņķis projicējas nesagrozīti arī tad, ja tikai viena tā mala ir paralēla projekciju plaknei.

Plaknes

Plakni telpā var noteikt trīs punkti, kas neatrodas uz vienas taisnes, vai divas krustiskas taisnes, vai divas paralēlas taisnes, vai taisne un punkts ārpus tās. Tāpat kā taisnes arī plaknes iedala vispārīgās un speciālās stāvotnes plaknēs, un tās veido attiecīgus leņķus ar attiecīgām projekciju plaknēm.

Taisnes, kas atrodas plaknē un ir paralēlas vienai no projekciju plaknēm, sauc par plaknes galvenajām taisnēm.

Starp plakni un taisni iespējamas tādas pašas stāvotnes kā starp divām taisnēm. Divas plaknes var būt savstarpēji paralēlas vai krustoties (tostarp krustoties perpendikulāri).

Līknes un virsmas

Plaknes līknes veidojas kā punkta trajektorija, punktam pārvietojoties plaknē, šādu līkņu visi punkti atrodas vienā plaknē. Līknes var būt likumsakarīgas vai grafiskas. Likumsakarīgām līknēm ir zināmi to veidošanās likumi, kuri parasti izteikti ar matemātiskiem vienādojumiem. Šīs līknes atkarībā no vienādojuma iedala algebriskās līknēs (riņķis, elipse, parabola, hiperbola, kardioīda u.c.) un nealgebriskās līknēs (Arhimēda spirāle, evolvente, sinusoīda, cikloīda u.c.). Grafiskas līknes noteiktas tikai ar projekcijām un tajās nav saskatāma matemātiska likumsakarība.

Telpas līknēm ir trīs dimensijas. Liektu virsmu krustošanās līnijas ir telpas līknes. Līknei ģeometriski var noteikt kārtu, piemēram, elipsei un taisnei lielākais iespējamais krustpunktu skaits ir divi, tātad elipse ir otrās kārtas līkne.

Viena no telpisko objektu veidošanas metodēm ir uzdošana ar norobežojošām virsmām, tēlotājā ģeometrijā tā ir kinemātiskā veidošanas metode, pēc kuras, virsma ir kādas līnijas secīgu stāvokļu kopums, šai līnijai pārvietojoties telpā. Virsmu veidojošā līnija kustībā var nemainīties vai nepārtraukti mainīties pēc noteikta likuma. Kāda virsma var tikt veidota, kādai līnijai, ko sauc par veidojošo līniju jeb veiduli, pārvietojoties pa nekustīgu līniju, ko sauc par vadošo līniju jeb vaduli. Lai virsmu uzdotu kompleksajā rasējumā, tajā attēlo virsmu veidojošo elementu ortogonālās projekcijas un norāda virsmu veidojošās līnijas kustības likumu. Virsmas neatkarīgu elementu kopu, kas nosaka doto virsmu, sauc par virsmas noteicēju, kurš sastāv no grafiskās daļas un no līnijas kustības likuma.

Ja kādu virsmu ortogonāli projicē uz projekciju plaknes, tad projicējošās taisnes, kas pieskaras virsmai, veido cilindrisku vai prizmatisku virsmu. Projicējošās taisnes pieskaras projicējamajai virsmai punktos, kuri veido kontūrlīniju. Kontūrlīnijas projekcija uz projekciju plaknes ir apveida līnija.

Virsmas var būt noslēgtas (telpas punktu ieslēdz tā, ka tas nevar izkļūt ārpusē, nekrustojot doto virsmu) un nenoslēgtas.

Virsmas veidošanas paņēmienus var iedalīt pēc veidules kustības likuma — virsmas ar paralēlo veidules pārbīdi, virsmas ar veidules rotāciju, virsmas ar veidules vītņveida kustību —, pēc veidules veida — virsmas ar taisnu veiduli, virsmas ar līku veiduli —, pēc veidules formas maiņas likuma — virsmas ar nemainīgu veidules formu, virsmas ar mainīgu veidules formu —, pēc virsmas savietojamības ar plakni — izklājamās virsmas, neizklājamās virsmas —, pēc virsmas uzdošanas likuma: analītiski, ģeometriski.

Virsmu iedalījums ir šāds. Ir kinemātiski veidotas virsmas, kurās ietilpst taišņu virsmas (veidojas, taisnei pārvietojoties telpā; šeit ietilpst arī vītņveida virsmas), līkņu virsmas (veidojas, līknei pārvietojoties telpā; šeit iederas arī bīdvirsmas, kas veidojas, nemainīgai plaknes vai telpas līknei pārvietojoties telpā paralēli sev), cikliskas virsmas (veidojas, veidulei riņķa līnijai ar nemainīgu vai mainīgu rādiusu pārvietojoties telpā, pie tām pieder kanālvirsmas, kas veidojas, veidulei riņķa līnijai ar mainīgu rādiusu pārvietojoties tā, ka tās centrs slīd pa līkni vaduli, bet riņķa plakne paliek perpendikulāra vadulei, un cauruļvirsmas, kas veidojas līdzīgi kā kanālvirsmas, taču to riņķa līniju veiduļu rādiuss ir pastāvīgs), izvērstās virsmas (veidojas, patvaļīgas formas veidulei ar nemainīgu vai mainīgu profilu pārvietojoties telpā pēc brīvi izvēlēta ģeometriska likuma. Rotācijas virsmas, kas veidojas, patvaļīgas formas veidulei rotējot ap nekustīgu asi, attiecas gan pie taišņu, gan pie līkņu virsmām. Ir karkasa virsmas, kuras uzdod ar divām līniju kopām un kurās ietilpst virsmas ar līniju karkasu (ietver tīklveida virsmas, topogrāfiskās virsmas, grafiskās virsmas) un virsmas ar punktu karkasu (ietver grafiskās virsmas). Topogrāfiskās virsmas neveido pēc noteiktiem ģeometriskiem likumiem. Praksē visbiežāk izmanto taišņu un rotācijas virsmas.

Taišņu virsmas, kurām ir vienkāršs kinemātiskais veidošanās likums, veidojas šādi. Cilindriskas un prizmatiskas virsmas veidojas, veidulei (taisnei) pārvietojoties pa vaduli, paliekot paralēlai pašai sev. Ja vadule ir noslēgta līkne, veidojas noslēgta cilindriska sānu virsma. Ja vadule ir taisne, iegūst plakni. Ja vadule ir noslēgta lauzta līnija, veidojas noslēgta prizmatiska sānu virsma. Koniskas un piramidālas virsmas veidojas, taisnei slīdot pa vaduli un ejot caur nekustīgu punktu, kas ir dotās virsmas virsotne. Koniskas virsmas vadule ir riņķa līnija, piramidālas virsmas vadule ir lauzta līnija.

Pie taišņu virsmām ar sarežģītu kinemātisko veidošanās likumu pieder greizā plakne (hiperboliskais paraboloīds), kura veidojas, veidulei pārvietojoties pa divām šķērsām vadulēm, tai paliekot paralēlai virziena plaknei.

Rotācijas virsmas forma atkarīga no veidojošās līnijas formas. Ja ap asi rotē patvaļīga līnija, veidojas rotācijas virsma, kuras veidules punkts, rotējot ap asi, apraksta riņķa līniju uz rotācijas virsmas, ko sauc par paralēli; vismazāko paralēli sauc par kaklu, vislielāko — par ekvatoru; virsmas līnijas, kuru plaknes iet caur rotācijas asi, sauc par meridiāniem; projekciju plaknei paralēlu meridiānu sauc par galveno meridiānu. Ja ap asi rotē tai paralēla taisne, veidojas cilindrs. Ja ap asi rotē taisne, kas krusto asi vienā punktā (virsotnē), veidojas konuss. Ja taisne rotē ap asi, kura ir šķērsa šai taisnei, veidojas viendobuma hiperboloīds. Ja rotācijas virsmas veidule ir riņķa līnija, veidojas trīs dažādas virsmas. Ja puse no riņķa līnijas rotē ap savu diametru, rodas sfēras virsma. Riņķa līnijai rotējot ap asi, kas atrodas riņķa līnijas plaknē, bet neiet caur tās centru, rodas tora virsma. Riņķa līnijai rotējot ap asi, kas atrodas riņķa līnijas plaknē, bet nekrusto to, veidojas gredzena virsma.

Ģeometrisks objekts ir projicējošs pret projekciju plakni, ja tā projekcija šajā plaknē ir par vienu dimensiju zemāka nekā pats objekts. Punkts ir 0 dimensiju obkjekts, līnija ir 1 dimensijas obekts, virsma ir 2 dimensiju objekts. Virsmas projekciju (horizontālo, frontālo vai profilo), kurā virsma attēlojas par taisni, sauc par virsmas galveno jeb koncentrējošo projekciju.

Daudzskaldņi

Daudzskaldņi ir objekti, kas no visām pusēm norobežoti ar plakaniem daudzstūriem, kurus sauc par skaldnēm. Divu skaldņu krustošanās līniju sauc par šķautni. Triju vai vairāku šķautņu krustpunktu sauc par virsotni. Inženiergrafikā bieži sastopami daudzskaldņu šķēlumi, tāpēc nepieciešams konstruēt šķēlumu projekcijas. Šķēlums ir figūra, kuru iegūst, iedomāti šķeļot objektu ar plakni. Daudzskaldņa škēlums ir daudzstūris, kura virsotnes daudzskaldņa šķautņu un šķēlējplaknes krustpunkti, malas — daudzskaldņa skaldņu un šķēlējplaknes taišņu nogriežņi. Lai attēlotu daudzstūru — prizmas, piramīdas — šķēlumu, jāatrod šī šķēluma virsotņu projekcijas, izmantojot kārtotājas taisnes, kā arī nepieciešamības gadījumā palīgtaisnes vai proporcionālo dalīšanu.

Pēc šķelšanas iegūtā ķermeņa redzamās šķautnes attālo ar pamatlīnijām (platām līnijām), neredzamās šķautnes (tās, kuras ir iegūtajam ķermenim, bet nav redzamas skatītājam dotajā novietojumā) attēlo ar svītrlīniju, atšķeltās un, tā teikt, "atmestās" šķautnes vai to daļas var parādīt ar palīglīnijām (tievām līnijām).

Daudzskaldņi var tikt šķelti ar vairākām plaknēm, veidojot tajos izgriezumus.

Cilindra šķēlumi

Konusa šķēlumi

Rotācijas ķermeņi

Kompleksajā rasējumā šķēluma līniju konstruē, izmantojot atsevišķus tās punktus, daži šķēluma līnijas punkti ir īpaši: ekstremālie punkti atrodas vistālāk no kādas projekciju plaknes vai vistuvāk tai, redzamības maiņas punkti atdala šķēluma redzamo un neredzamo daļu (tie vienmēr atrodas uz virsmas projekcijas kontūrlīnijām), tāpat ir punkti, kas, konstruējot elipsi (šķēluma līniju cilindram vai konusam), nosaka tās lielo un mazo asi. Pārējos šķēluma līnijas punktus sauc par starppunktiem (savienojot pietiekamu skaitu starppunktu ar lekālu, iegūst, piemēram, pareizu elipsi).

Rotācijas ķermeņi ir objekti, kas rodas, plaknes figūrai griežoties ap asi. Šķēlums, kas veidojas, plaknei šķeļot rotācijas cilindru, ir atkarīgs no leņķa starp šķēlejplakni un cilindra rotācijas asi. Cilindra šķēluma līnija var būt divas veidules (plakne paralēla asij un veidulēm, figūra — taisnstūris), riņķa līnija (plakne perpendikulāra asij), elipse (plakne slīpa pret asi un šķeļ visas veidules) vai tās daļa (plakne nešķeļ visas veidules).

Cilindra un nošķelta konusa krustošanās

Rotācijas konusa virsmas un plaknes šķēluma līnijas ir otrās kārtas līnijas. Ja šķēlējplakne iet caur konusa virsotni, šķēluma figūra ir trijstūris. Ja šķēlējplakne ir perpendikulāra konusa rotācijas asij, šķēluma figūra ir riņķis. Apzīmējot ar λ leņķi starp šķēlējplakni un konusa rotācijas asi un ar φ leņķi starp konusa veiduli un rotācijas asi, var izšķirt šādus šķēluma līnijas gadījumus: λ>φ — elipse, λ=φ — parabola, λ<φ vai λ=0 — hiperbola.

Lodes virsmas un jebkuras plaknes šķēluma līnija ir riņķa līnija. Ja šķēlējplakne iet caur lodes centru, tad riņķa līnijas rādiuss ir vienāds ar lodes rādiusu. Jo tālāk no lodes centra atrodas šķēlējplakne, jo mazāks rādiuss.

Ja krustojas divas rotācijas virsmas un jākonstruē to krustošanās līnija — telpiska līkne —, tad abu virsmu kopējos punktus nosaka ar palīgvirsmu metodi. Šajā metodē palīgvirsma (tā var būt palīgplakne vai palīgsfēra) šķeļ abas virsmas, iegūstot divas šķēlumu līnijas, kuras pieder divām dažādām virsmām, taču atrodas uz kopīgas trešās virsmas (palīgvirsmas). Abu šķēluma līniju krustpunkti norāda abu virsmu kopīgos punktus. Lai šķēluma līniju uzkonstruētu precīzi, izmanto vairākas palīgvirsmas, tādējādi atrodot vairāk krustpunktu. Palīgplakņu metodi var izmantot jebkuru virsmu krustošanās līniju attēlošani, taču to ērti lietot tikai tad, ja palīgplaknes un katras virsmas šķēluma līnijas ir taisnes vai riņķa līnijas (vienkārši konstruējamas). Pārējos gadījumos (šķēluma līnijas nav vienkārši konstruēt) izmanto palīgsfēru metodi. Īpašs krustošanās gadījums ir tad, ja krustojas divas virsmas, kurām ir kopīga ievilkta vai apvilkta lode. Tad krustošanās līnija sadalās divās otrās kārtas līknēs. To apraksta Monža teorēma.