Determinants

Lineārajā algebrā determinants ir lielums, ko var piekārtot jebkurai kvadrātveida matricai. Matricas A determinantu parasti apzīmē ar det(A) vai |A| un to var izteikt kā polinomu no matricas A elementiem.

Definīcija

Aksiomātiska definīcija

Determinants ir definēts jebkurai kvadrātveida matricai pār komutatīvu gredzenu R (piemēram, veseli, reāli vai kompleksi skaitļi). Funkciju ƒ: R^n×n → R, kas n×n matricām pār gredzenu R piekārto elementus no R, sauc par determinantu, ja tai izpildās šādas trīs īpašības:

1. ƒ(I) = 1, kur I ir n×n vienības matrica (šeit 1 apzīmē gredzena R vienības elementu),
2. funkcija ƒ ir lineāra attiecībā pret matricas rindiņām (skatīt zemāk),
3. ƒ(A) = 0, ja jebkuras divas matricas A rindiņas ir vienādas (šeit 0 apzīmē gredzena R nulles elementu).

Var pierādīt, ka eksistē viena vienīga funkcija ƒ, kurai izpildās šīs trīs īpašības. Šo funkciju parasti apzīmē ar "det".

Linearitāte

Ja A ir n×n matrica un ar r_i apzīmē rindas vektoru, kas vienāds ar šīs matricas i-to rindiņu, tad matricu A var pierakstīt šādi:

$A = \begin{bmatrix} r_1 \\ r_2 \\ \vdots \\ r_n \end{bmatrix}.$

Funkciju ƒ: R^n×n → R sauc par lineāru attiecībā pret matricas rindiņām, ja tai izpildās šāda īpašība:

$f \begin{pmatrix} \begin{bmatrix} r_1 \\ r_2 \\ \vdots \\ \alpha r_i + \beta r'_i \\ \vdots \\ r_n \end{bmatrix} \end{pmatrix} = \alpha f \begin{pmatrix} \begin{bmatrix} r_1 \\ r_2 \\ \vdots \\ r_i \\ \vdots \\ r_n \end{bmatrix} \end{pmatrix} + \beta f \begin{pmatrix} \begin{bmatrix} r_1 \\ r_2 \\ \vdots \\ r'_i \\ \vdots \\ r_n \end{bmatrix} \end{pmatrix},$

kur α un β ir patvaļīgi gredzena R elementi un i ir vesels skaitlis no 1 līdz n.

Formula 2×2 matricām

$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a d - b c.$

Formula 3×3 matricām

Metode determinanta aprēķināšanai 3×3 matricai.

$\begin{align} \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} &= a \begin{vmatrix} e & f \\ h & i \end{vmatrix} - b \begin{vmatrix} d & f \\ g & i \end{vmatrix} + c \begin{vmatrix} d & e \\ g & h \end{vmatrix} \\ &= a (ei - fh) - b (di - fg) + c (dh - eg) \\ &= a e i + b f g + c d h - c e g - b d i - a f h. \end{align}$

Piemēram, ja

$A = \begin{pmatrix} -2 & 2 & -3 \\ -1 & 1 & 3 \\ 2 & 0 & -1 \end{pmatrix}$

tad

$\begin{align} \det(A) &= \bigl( (-2) \cdot 1 \cdot (-1) \bigr) + \bigl( 2 \cdot 3 \cdot 2 \bigr) + \bigl( (-3) \cdot (-1) \cdot 0 \bigr) \\ &- \bigl( 2 \cdot 1 \cdot (-3) \bigr) - \bigl( 0 \cdot 3 \cdot (-2) \bigr) - \bigl( (-1) \cdot (-1) \cdot 2 \bigr) \\ &= 2 + 12 + 0 - (-6) - 0 - 2 = 18. \end{align}$

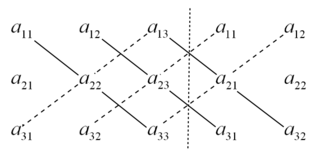
Lai aprēķinātu determinantu 3×3 matricai, var izmantot Sarusa metodi.

Formulas n×n matricām

Determinantu n×n matricai

$A = \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,n} \end{pmatrix}$

var izteikt kā polinomu no tās elementiem a_i,j. Šo polinomu parasti apzīmē ar det(A) un tas satur n! saskaitāmos. Katrs no šiem saskaitāmajiem ir vai nu ar plus vai mīnus zīmi un sastāv no n matricas Aelementu reizinājuma (pa vienam no katras rindas un kolonnas). Šo polinomu var izteikt ar vairāku ekvivalentu formulu palīdzību.

Leibnica formula

Bieži vien determinantu definē ar Leibnica formulas palīdzību:

$\begin{align} \det(A) &= \sum_{\sigma \in S_n} \sgn(\sigma) a_{1,\sigma(1)} a_{2,\sigma(2)} \cdots a_{n,\sigma(n)} \\ &= \sum_{\sigma \in S_n} \sgn(\sigma) \prod_{i=1}^n a_{i,\sigma(i)}. \end{align}$

Šajā formulā S_n apzīmē simetrisko grupu jeb kopu, kas sastāv no visām n elementu permutācijām, sgn(σ) ir permutācijas σ zīme, σ(i) ir skaitlis no 1 līdz n, uz kuru σ attēlo i.

Intuitīvi par permutāciju σ var domāt kā par virkni garumā n, kas satur skaitļus no 1 līdz n patvaļīgā secībā tā, ka katrs skaitlis parādās tieši vienu reizi; S_n ir kopa no visām šādām virknēm, σ(i) ir i-tais skaitlis virknē σ, bet zīme sgn(σ) ir vienāda ar +1 vai -1, atkarībā no tā vai virknē σ esošos skaitļus nepieciešams mainīt vietām pāra vai nepāra skaitu reižu, lai to sakārtotu augošā secībā.

Summa ar Levi-Čivita simbolu

Leibnica formulā esošā summa ir pār visām virknēm σ garumā n, kurā katrs no skaitļiem no 1 līdz n parādās tieši vienu reizi. Šo summu var pārrakstīt tā, lai tajā parādītos visas iespējamās virknes garumā n (tā satur skaitļus no 1 līdz n un katrs no tiem drīkst parādīties patvaļīgi daudz reižu — sākot no nevienas, līdz pat n reizēm). Šī summa sastāv no nⁿ saskaitāmajiem, taču lielākā daļa no tiem ir vienāda ar nulli:

$\begin{align} \det A &= \sum_{i_1 ,i_2, \ldots, i_n = 1}^n \varepsilon_{i_1 i_2 \dots i_n} a_{1,i_1} a_{2,i_2} \cdots a_{n,i_n} \\ &= \sum_{i_1 ,i_2, \ldots, i_n = 1}^n \varepsilon_{i_1 i_2 \dots i_n} \prod_{k=1}^n a_{k,i_k}. \end{align}$

Šajā formulā $\varepsilon_{i_1 i_2 \dots i_n}$ ir Levi-Čivita simbols, kas ir vienāds ar 0, ja virkne i₁i₂…i_n nav permutācija, bet pretējā gadījumā ir vienāds ar šīs permutācijas zīmi.

Laplasa formula

Ja A = (a_1,1) ir 1×1 matrica, tad det(A) = a_1,1. Lielākām matricām determinantu var aprēķināt rekursīvi ar Laplasa formulas palīdzību. Tā izsaka dotās matricas determinantu kā funkciju no mazāku apakšmatricu determinantiem. Šo procesu sauc par determinanta izvirzīšanu pēc attiecīgās rindiņas vai kolonnas:

$\begin{align} \det(A) &= \sum_{j=1}^n (-1)^{i+j} a_{i,j} M_{i,j} \\ &= \sum_{i=1}^n (-1)^{i+j} a_{i,j} M_{i,j}. \end{align}$

Pirmajā izteiksmē indekss i ir fiksēts un tā atbilst izvirzījumam pēc i-tās rindiņas, bet otrajā izteiksmē indekss j ir fiksēts un tā atbilst izvirzījumam pēc j-tās kolonnas. Šajās formulās M_i,j apzīmē determinantu apakšmatricai, kas iegūta atmetot matricas A i-to rindiņu un j-to kolonnu (šos lielumus sauc par matricas A minoriem).

Determinanta ģeometriskā interpretācija

Laukums paralelogramam, kuru veido vektori (a,b) un (c,d).

Paralelograma laukums ir vienāds ar determinanta absolūto vērtību matricai, kas sastāv no paralelogramu veidojošajiem vektoriem.

Skatīt arī

• Permanents

Papildu literatūra

Latviski:

Angliski:

• Lang, Serge (1987), Linear algebra, Undergraduate texts in mathematics (3 izd.), Springer, ISBN 978-0-38-796412-6 , Nodaļa VI, Determinants, 140. lpp.
• Lang, Serge (1986), Introduction to Linear algebra, Undergraduate texts in mathematics (2 izd.), Springer, ISBN 978-0-38-796205-4 , Nodaļa VII, Determinants, 195. lpp.

Vāciski:

• Artin, Michael (1998), Algebra, Grundstudium Mathematik (2 izd.), Birkhäuser, ISBN 978-3-76-435938-6 , Nodaļa 1.3, Determinanten, 20. lpp.

Ārējās saites

• Eric W. Weisstein, Determinant, MathWorld.