Mērīšana

Mērīšana ir process, kad kvantitatīvi (skaitliski) salīdzina divus vienādas dabas lielumus, no kuriem viens ir mērāmais objekts, bet otrs ir izvēlētā mēra vienība — mērvienība. Ar mērīšanu nosaka lielumu (piemēram, garums, vielas koncentrācija, ātrums, ekspozīcijas doza un citi) skaitlisko vērtību, un to veic ar mērinstrumentu palīdzību, bet tajā pašā laikā mērījumu var veikt vienkārši skaitot, nosakot doto objektu skaitu. Plašākā nozīmē mērīšana ir dažādu objektu, priekšmetu, parādību salīdzināšana pēc noteiktas vērtības vai parametra.

Mērīšanas veidi

Mērīšanu var veikt divos veidos, tas ir, tieši izmērot fizikālo lielumu, vai arī netieši, izmērot citus lielumus, un tikai tad noskaidrojot mērāmā lielumu skaitlisko vērtību.^[1]

Tiešā mērīšana

Tiešajā mērīšanā mērījumu iegūst, uzreiz to nolasot no mērierīces. Atkarībā no tā, vai vērtība tiek iegūta tieši no mērierīces rādījuma vai pēc izmēra novirzes no iestatītā mēra, tiešo mērīšanu iedala absolūtajā (mērījumu nolasa kā mērierīces rādījumu) un relatīvajā mērīšanā (mērījumu iegūst, summējot iestatīto izmēru un mērierīces uzrādīto rādījumu, kas ir novirze no iestatītā izmēra). Relatīvo mērīšanu izdevīgi lietot lielsēriju ražošanā.

Tiešā mērīšana ir arī priekšmetu skaitīšana.

Skaitīšana

Nogriežņa izmērīšana, skaitot nogriežņu CD skaitu

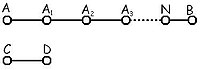
Kā skaitīšanas piemēru var minēt nogriežņa AB mērīšana. Par mēra vienību tiek pieņemts nogrieznis CD un, sākot no punkta A, pakāpeniski tiek atlikts nogrieznis CD uz nogriežņa AB tā, lai CD=AA₁=A₁A₂=...=A_n-1N. Tad ir iespējami divi varianti:

nogrieznis CD ietilpst nogrieznī AB n reizes bez atlikuma, t.i., punkts N sakrīt ar punktu B;
punkts N nesakrīt ar punktu B (kā zīmējumā) un rodas atlikums, kas ir mazāks par CD.

Pirmajā gadījumā nogriežņa AB garumu izsaka naturāls skaitlis n.

Otrā, vispārīgajā gadījumā uz nogriežņa NB analogi atliksim nogriežņa CD vienu desmitdaļu, t.i., tādu nogriezni, kurš ir 10 reizes ietilpst mēra vienībā CD. Ja mēra vienības desmitdaļa ietilpst pirmajā atlikumā NB n₁ reizi un rodas jauns atlikums, tad to savukārt mēra ar mēra vienības vienu simtdaļu utt.

Vispārīgā gadījumā nogriežņa AB garumu izsaka skaitlis

{\frac {AB}{CD}}=n,n_{1}n_{2}n_{3}...\

Šis skaitlis ir decimāldaļa, kurā ir n veselu, n₁ desmitdaļu, n₂ simtdaļu, n₃ tūkstošdaļu utt.

Ja n,n₁n₂n₃... ir galīga decimāldaļa vai arī bezgalīga, bet periodiska decimāldaļa (kuru vienmēr var pārvērst vienkāršā daļā), tad saka, ka nogriežņi AB un CD ir samērojami un mērīšanas rezultāts ir racionāls skaitlis. Tātad naturāls skaitlis ir racionāla skaitļa speciāls gadījums.

Ja n,n₁n₂n₃... ir bezgalīga, neperiodiska decimāldaļa, tad saka, ka nogriežņi AB un CD ir nesamērojami un mērīšanas rezultāts ir iracionāls skaitlis.

Netiešā mērīšana

Netiešajā mērīšanā tiek izmantoti citi lielumi, lai aprēķinātu mērāmo lielumu. Piemēram, ar ampērmetru izmērot strāvas stiprumu un ar voltmetru izmērot elektrisko spriegumu, var aprēķināt un noteikt elektrisko pretestību. Parasti tiek izmantota kāda jau iepriekš zināma sakarība, formula. Šāda mērīšana ir neprecīza, tāpēc pēc iespējas ir veicama tiešā mērīšana.

Mērvienības

Pamatraksts: mērvienība

Mērvienības tiek izmantotas, lai noteiktu kāda fizikālā lieluma skaitlisko vērtību. Pasaulē tiek izmantotas dažnedažādas mērvienības, tādēļ ir panākta vienošanās, kas nosaka, ka zinātniskajā vidē tiek izmantota Starptautiskā mērvienību sistēma (SI). Tajā ir noteiktas septiņas SI pamatvienības, no kurām var iegūt jebkuru citu mērvienību.

Mērīšanas kļūdas

Ikvienam mērījumam piemīt mērījuma kļūda. Fizikālā lieluma vērtību, kas bez mazākās kļūdas raksturo kādu ķermeni vai norisi, sauc par patieso vērtību. Praktiski tā nav iegūstama. Par reālo vērtību sauc tādu vērtību, kas ir praktiski izmērāma un ir tuva patiesajai vērtībai. Par absolūto kļūdu $\Delta x$ sauc mērīšanas gaitā iegūtā rezultāta $x'$ un lieluma reālās vērtības $x$ starpību:

$\Delta x=x'-x$ .

Absolūtās kļūdas attiecību pret reālo vērtību sauc par relatīvo kļūdu

$\varepsilon ={\frac {\Delta x}{x}}\cdot 100$ %.

Pēc izcelsmes izšķir šādas kļūdas, kuras kopā veido absolūto kļūdu:

rupja kļūda var ieviesties mērinstrumenta rādījumu nepareizas nolasīšanas, nolasīto vērtību nepareizas pierakstīšanas, nepamanītu mērīšanas apstākļu izmaiņu un citu līdzīgu iemeslu dēļ,
sistemātiskās kļūdas jēdzienā ietilpst:
- korekcija, kuras vērtība ir zināma, piemēram, kad mērierīce vēl pirms mērījuma sākšanas uzrāda noteiktu vērtību (sākumnolasījums nav 0),
- mērinstrumenta kļūda — saistīta ar mērinstrumenta ierobežoto precizitāti, tās precīza vērtība nav zināma, taču to aizstāj ar mērinstrumenta pamatkļūdu,
- objekta kļūda — saistīta ar mērāmā objekta īpatnībām (piemēram, pēc izmērītas metāliska priekšmeta masas un tilpuma, aprēķinot iegūst aplamu šī priekšmeta blīvumu, nezinot, ka iekšienē tas ir dobs);
gadījuma kļūda ir daļa absolūtās kļūdas, bet tās daudzie cēloņi nav zināmi.

Kļūdu ietekmi uz mērījumu precizitāti mazina:

novēršot rupju kļūdu rašanās cēloņus vai izslēdzot tās no iegūtajiem rezultātiem,
ievērojot nepieciešamās korekcijas,
novēršot objekta kļūdas,
novērtējot nenovēršamās mērinstrumenta un gadījuma kļūdas un veicot mērīšanu vairākkārtīgi.

Mērījuma precizitātes nodrošināšana

Lai nodrošinātu minimālo precizitāti, viens izmērs jāmēra vismaz trīs reizes. Mērot lineāros izmērus vienai detaļai, mērījumi tiek veikti trīs šķēlumos divās perpendikulārās plaknēs — iegūst 6 izmērus, veikti 18 mērījumi. Izmantojot šos izmērus, matemātiski var noteikt formas novirzes un reālo izmēru.

Mērījumiem ar mehānisko kontaktu jāizvēlas atbilstoša mērtausta vai tā uzgaļa forma, lai saskarvirsma starp mērāmā priekšmeta virsmu un mērtaustu būtu punkts: sfērisks mērtausts plakanām virsmām, cilindriskām virsmām — nažveida, sfēriskām virsmām — plakans.

Veicot ģeometriskos mērījumus ražojumu izmēru kontrolei, mērinstrumenta precizitātei jābūt pietiekoši augstai salīdzinājumā ar kontrolējamā izstrādājuma izgatavošanas precizitāti.

Lineāriem mērījumiem pēc iespējas jāievēro Abes princips. Jāņem vērā mērīšanas spēka un ārējo faktoru, piemēram, temperatūras, ietekme.

Mērīšanas izmantošana

Mērījumi ir nepieciešami ļoti daudzās zinātnes nozarēs, piemēram, fizikā, ķīmijā, ģeogrāfijā un citās nozarēs. Jo tie ir precīzāki un lielākā skaitā, jo lielāka iespēja novest risinājumu tuvāk patiesībai.