Elektriskais lauks

Elektrodinamika

Elektrodinamikas pamatvienādojumi

1. Maksvela diferenciālvienādojumi

1.1. Integrālie Maksvela vienādojumi

2. Elektriskais lauks

2.1. Gausa teorēma (Elektriskā lauka plūsma)

2.2. Elektriskā lauka cirkulācija

2.3. Kulona likums

2.4. Elektriskā strāva

2.5. Strāvas nepārtrauktības vienādojums

2.6. Pilnās strāvas nepārtrauktības vienādojums

2.7. Nobīdes strāva

2.8. Elektriskā lādiņa nezūdamības likums

2.9. Elektromagnētiskās indukcijas likums

3. Magnētiskais lauks

3.1. Magnētiskās indukcijas plūsma

3.2. Magnētiskās indukcijas cirkulācija

3.3. Lorenca spēks

4. Elektromagnētiskā lauka avoti

5. Elektromagnētiskā lauka enerģija

6. Delta funkcija

Elektriskais lauks ir lauks, kas pastāv ap jebkuru elektriski lādētu ķermeni vai lādiņu, un Kulona likumu var interpretēt šādi: viens no lādiņiem, piemēram $q_2 = q \$, ir lauka avots, bet otrs, $q_1 \$, atrodas tā radītajā laukā un uz to darbojas Kulona spēks $\vec{F} \$.

Elektriskā lauka intensitāte

Elektriskā lauka intensitāte jeb elektriskā lauka intensitātes vektors $\vec{E} \$ raksturo elektrisko lauku katrā telpas punktā. Elektriskā lauka intensitāte ir Kulona spēks $\vec{F} \$, kurš pielikts vienu kulonu lielam pozitīvam punktveida lādiņam.

Skalārā forma

$\vec{E} = \frac {\vec{F}}{q_1} \$

kur

$\vec{E} \$ ir elektriskā lauka intensitāte (N/C)

$\vec{F} \$ ir Kulona spēks (N)

$q_1 \$ ir lādiņš, uz kuru iedarbojas spēks (C)

Elektriskā lauka intensitātes vektori (zilā krāsā) ir vērsti prom no pozitīva lādiņa, savukārt tie ir vērsti virzienā uz negatīvu lādiņu. Jo tālāk no lādiņa, jo intesitātes vektora modulis ir mazāks.

No Kulona likuma izriet, ka

$\vec{E} = k \frac{q q_1}{r^2 q_1} = k \frac {q}{r^2} \$, tātad $\vec{E} = k \frac {q}{r^2} \$

kur

$q \$ šoreiz ir lādiņš, kurš rada elektrisko lauku (C)

$r \$ ir attālums no lādiņa (m)

$k = \frac{1}{4 \pi \epsilon_0} \approx 8,988 \cdot 10^9$ N m² C^-2

Vektoriālā forma

$\vec{E}(\vec{r}) = \frac {\vec{F}(\vec{r})}{q_1} \$

kur

$\vec{E} \$ ir elektriskā lauka intensitāte (N/C)

$\vec{F} \$ ir Kulona spēks (N)

$q_1 \$ ir lādiņš, uz kuru iedarbojas spēks (C)

$\vec{r} \$ ir rādiusvektors no koordinātu sistēmas sākumpunkta līdz intensitātes vai spēka vektora pielikšanas punktam (m)

No Kulona likuma izriet, ka

$\vec{E}(\vec{r}) = k \frac{q q_1}{r^3 q_1} \vec{r} = k \frac {q}{r^3} \vec{r}\$, tātad $\vec{E}(\vec{r}) = k \frac {q}{r^3} \vec{r}\$

kur

$q \$ šoreiz ir lādiņš, kurš rada elektrisko lauku (C)

$\vec{r} \$ ir rādiusvektors no lādiņa (m)

$k = \frac{1}{4 \pi \epsilon_0} \approx 8,988 \cdot 10^9$ N m² C^-2

Elektriskā lauka cirkulācija

Elektriskās intensitātes cirkulācija pa ceļu $l \$ ir darbs $A \$.

$A = \int_l \vec{E} \mathrm{d} \vec{r} \$

kur

$\vec{E} \$ - elektriskā lauka intensitāte (N/C)

$\mathrm{d} \vec{r} \$ - rādiusvektora izmaiņa (m)

Secinājums, ka elektriskā lauka cirkulācija ir darbs, izriet no tā, ka pēc definīcijas elektriskā lauka intensitāte ir spēks, kurš darbojas uz vienības punktveida lādiņu, un šis pozitīvais vienības lādiņš pārvietojas elektriskajā laukā $\vec{E} \$ pa ceļu $l \$.

Galvenais raksts Elektriskā lauka cirkulācija

Elektromagnētiskās indukcijas likums

Elektromagnētiskās indukcijas likums ir

$\epsilon_i = \frac{\Delta \Phi}{\Delta t} \$

kur

$\epsilon_i \$ ir indukcijas elektrodzinējspēks, kuru rada mainīga magnētiskā plūsma V)

$\Delta \Phi \$ ir magnētiskās plūsmas izmaiņa (Wb)

$\Delta t \$ ir laiks, kurā notiek magnētiskās plūsmas izmaiņa (s)

Vairāk par elektromagnētiskās indukcijas likumu skatīt šeit

Elektriskā lauka plūsma

$N = \oint_S \vec{E} \cdot \mathrm{d}\vec{S} = \frac{q}{\epsilon_0} \$

kur

$N \$ - elektriskā lauka intensitātes plūsma (C×m/F vai V*m)

$\vec{E} \$ - elektriskā lauka intensitāte (N/C)

$\vec{S} \$ - virsmas vektors (m²)

$q \$ - lādiņš, kurš rada elektrisko lauku (C)

$\epsilon_0 \approx$ 8,85×10^-12 F/m - elektriskā konstante

Vairāk par elektriskā lauka plūsmu skatīt šeit

Superpozīcijas princips

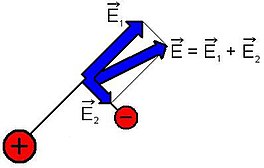
Superpozīcijas princips: vairāku avotu radītais elektriskais lauks $\vec{E} \$ jebkurā telpas punktā ir atsevišķu avotu lauku summa

$\vec{E} = \vec{E}_1 + \vec{E}_2 + ... + \vec{E}_n \$

Tas nozīmē, ka elektriskie lauki pārklājas viens otru neietekmējot.